(7532 + 100y2) + 10(10y2 − 110)
The expression above can be written in the form ay2 + b, where a and b are constants. What is the value of a + b?
-
Solution
The correct answer is 6632. Applying the distributive property to the expression yields 7532 + 100y2 + 100y2 − 1100. Then adding together 7532 + 100y2 and 100y2 − 1100 and collecting like terms results in 200y2 + 6432. This is written in the form ay2 + b, where a = 200 and b = 6432. Therefore a + b = 200 + 6432 = 6632.
The graph of a line in the xy-plane passes through the point (1,4) and crosses the x-axis at the point (2,0). The line crosses the y-axis at the point (0,b).What is the value of b ?
-
Solution
The correct answer is 8. Since the line passes through the point (2, 0), its equation is of the form y = m(x − 2). The coordinates of the point (1, 4) must also satisfy this equation. So 4 = m(1 − 2), or m = −4. Substituting −4 for m in the equation of the line gives y = −4(x – 2), or equivalently y = −4x + 8. Therefore, b = 8.
Alternate approach: Given the coordinates of two points through which the line passes, the slope of the line is \(\frac{4 − 0}{1 − 2}\) = −4. So, the equation of the line is of the form y = −4x + b. Since (2, 0) satisfies this equation, 0 = −4(2) + b must be true. Solving this equation for b gives b = 8.
The number of radians in a 720-degree angle can be written as aπ, where a is a constant. What is the value of a ?
-
Solution
The correct answer is 4. There are π radians in a 180° angle. A 720° angle is 4 times greater than a 180° angle. Therefore, the number of radians in a 720° angle is 4π.
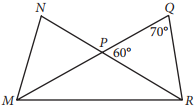
In the figure above, \(\overline{MQ}\) and \(\overline{NR}\) intersect at point P, NP QP = , and MP PR = . What is the measure, in degrees, of ∠QMR ? (Disregard the degree symbol when gridding your answer.)
-
Solution
The correct answer is 30. It is given that the measure of ∠QPR is 60°.Angle MPR and ∠QPR are collinear and therefore are supplementary angles. This means that the sum of the two angle measures is 180°, and so the measure of ∠MPR is 120°. The sum of the angles in a triangle is 180°. Subtracting the measure of ∠MPR from 180° yields the sum of the other angles in the triangle MPR. Since 180 − 120 = 60, the sum of the measures of ∠QMR and ∠NRM is 60°. It is given that MP = PR, so it follows that triangle MPR is isosceles. Therefore ∠QMR and ∠NRM must be congruent. Since the sum of the measure of these two angles is 60°, it follows that the measure of each angle is 30°.
An alternate approach would be to use the exterior angle theorem, noting that the measure of ∠QPR is equal to the sum of the measures of ∠QMR and ∠NRM. Since both angles are equal, each of them has a measure of 30°.
If 2 + 8 = 16 x , what is the value of x + 4 ?
-
Solution
The correct answer is 8. The expression 2x + 8 contains a factor of x + 4. It follows that the original equation can be rewritten as 2(x + 4) = 16. Dividing both sides of the equation by 2 gives x + 4 = 8.
The expression 1⁄3x2 − 2 can be rewritten as 1⁄3(x – k)(x + k), where k is a positive constant. What is the value of k ?
-
Solution
Factoring out the coefficient 1⁄3, the given expression can be rewritten as 1⁄3 (x2 − 6). The expression x2 – 6 can be approached as a difference of squares and rewritten as (x − √6 )(x + √6 ). Therefore, k must be √6.
Choice A is incorrect. If k were 2, then the expression given would be rewritten as 1⁄3 (x − 2)(x + 2), which is equivalent to 1⁄3 x2 − ⁄3, not 1⁄3 x2 − 2.
Choice B is incorrect. This may result from incorrectly factoring the expression and finding (x – 6) (x + 6) as the factored form of the expression. Choice C is incorrect. This may result from incorrectly distributing the 1⁄3 and rewriting the expression as 1⁄3 (x2 − 2).
A shipping service restricts the dimensions of the boxes it will ship for a certain type of service. The restriction states that for boxes shaped like rectangular prisms, the sum of the perimeter of the base of the box and the height of the box cannot exceed 130 inches. The perimeter of the base is determined using the width and length of the box. If a box has a height of 60 inches and its length is 2.5 times the width, which inequality shows the allowable width x, in inches, of the box?
-
Solution
If x is the width, in inches, of the box, then the length of the box is 2.5x inches. It follows that the perimeter of the base is 2(2.5x + x), or 7x inches. The height of the box is given to be 60 inches. According to the restriction, the sum of the perimeter of the base and the height of the box should not exceed 130 inches. Algebraically, that is 7x + 60 ≤ 130, or 7x ≤ 70. Dividing both sides of the inequality by 7 gives x ≤ 10. Since x represents the width of the box, x must also be a positive number. Therefore, the inequality 0 < x ≤ 10 represents all the allowable values of x that satisfy the given conditions.
Choices B, C, and D are incorrect and may result from calculation errors or misreading the given information.
Which of the following expressions is equivalent to \(\frac{x^{2}-2x-5}{x-3}\)?
-
Solution
The numerator of the given expression can be rewritten in terms of the denominator, x – 3, as follows:
x2 − 2x − 5 = x2 − 3x + x − 3 − 2, which is equivalent to
x(x – 3) + (x – 3) – 2. So the given expression is equivalent to \(\frac{x(x − 3) + (x − 3) − 2}{x − 3}=\frac{x(x − 3)}{x − 3}+\frac{x − 3}{x − 3}-\frac{2}{x − 3}\). Since the given expression is defined for x ≠ 3, the expression can be rewritten as \(x + 1 −\frac{2}{x − 3}\).Long division can also be used as an alternate approach.
Choices A, B, and C are incorrect and may result from errors made when dividing the two polynomials or making use of structure.
The function f is defined by f(x) = (x + 3)(x + 1). The graph of f in the xy-plane is a parabola. Which of the following intervals contains the x-coordinate of the vertex of the graph of f ?
-
Solution
The graph of a quadratic function in the xy-plane is a parabola. The axis of symmetry of the parabola passes through the vertex of the parabola. Therefore, the vertex of the parabola and the midpoint of the segment between the two x-intercepts of the graph have the same x-coordinate. Since f(–3) = f(–1) = 0, the x-coordinate of the vertex is \(\frac{(−3) + (−1)}{2}= –2\). Of the shown intervals, only the interval in choice B contains –2.
Choices A, C, and D are incorrect and may result from either calculation errors or misidentification of the graph’s x-intercepts.
The expression \(\frac{x^{-2}y^{\frac{1}{2}}}{x^{\frac{1}{3}}-1}\) , where x > 1 and y > 1, is equivalent to which of the following?
-
Solution
For x > 1 and y > 1, x1⁄3 and y1⁄2 are equivalent to \(\sqrt[3]{x}\) and √y , respectively. Also, x −2 and y −1 are equivalent to \(\frac{1}{x^{2}}\) and 1⁄y,respectively. Using these equivalences, the given expression can be rewritten as \(\frac{y\sqrt{y}}{x^{2}\sqrt[3]{x}}\).
Choices A, B, and C are incorrect because these choices are not equivalent to the given expression for x > 1 and y > 1.
For example, for x = 2 and y = 2, the value of the given expression is \(^{-\frac{5}{6}}\); the values of the choices, however, are 2\(^{-\frac{5}{6}}\), 2\(^{\frac{5}{6}}\), and 1, respectively