If a2 + b2 = z and ab = y, which of the following is equivalent to 4 +8 z y ?
-
Solution
Substituting a2 + b2 for z and ab for y into the expression 4z + 8y gives 4(a2 + b2) + 8ab. Multiplying a2 + b2 by 4 gives 4a2 + 4b2 + 8ab, or equivalently 4(a2 + 2ab + b2).Since (a2 + 2ab + b2) = (a + b)2, it follows that 4z + 8y is equivalent to (2a + 2b)2.
Choices A, C, and D are incorrect and likely result from errors made when substituting or factoring.
y = x2
2y + 6 = 2(x + 3)
If (x, y) is a solution of the system of equations above and x > 0, what is the value of xy ?
-
Solution
Substituting x2 for y in the second equation gives 2(x2) + 6 = 2(x + 3). This equation can be solved as follows:
2x2 + 6 = 2x + 6 (Apply the distributive property.)
2x2 + 6 − 2x − 6 = 0 (Subtract 2x and 6 from both sides of the equation.)
2x2 − 2x = 0 (Combine like terms.)
2x(x − 1) = 0 (Factor both terms on the left side of the equation by 2x.)
Thus, x = 0 and x = 1 are the solutions to the system. Since x > 0, only x = 1 needs to be considered. The value of y when x = 1 is y = x2 = 12 = 1. Therefore, the value of xy is (1)(1) = 1.
Choices B, C, and D are incorrect and likely result from a computational or conceptual error when solving this system of equations.
In air, the speed of sound S, in meters per second, is a linear function of the air temperature T, in degrees Celsius, and is given by ST(T) = 0.6T + 331.4. Which of the following statements is the best interpretation of the number 331.4 in this context?
-
Solution
The constant term 331.4 in S(T) = 0.6T + 331.4 is the value of S when T = 0. The value T = 0 corresponds to a temperature of 0°C. Since S(T) represents the speed of sound, 331.4 is the speed of sound, in meters per second, when the temperature is 0°C.
Choice B is incorrect. When T = 0.6°C, S(T) = 0.6(0.6) + 331.4 = 331.76, not 331.4, meters per second. Choice C is incorrect. Based on the given formula, the speed of sound increases by 0.6 meters per second for every increase of temperature by 1°C, as shown by the equation 0.6(T + 1) + 331.4 = (0.6T + 331.4) +0.6. Choice D is incorrect. An increase in the speed of sound, in meters per second, that corresponds to an increase of 0.6°C is 0.6(0.6) = 0.36.
Jackie has two summer jobs. She works as a tutor, which pays $12 per hour, and she works as a lifeguard, which pays $9.50 per hour. She can work no more than 20 hours per week, but she wants to earn at least $220 per week. Which of the following systems of inequalities represents this situation in terms of x and y, where x is the number of hours
she tutors and y is the number of hours she works as a lifeguard?
-
Solution
If Jackie works x hours as a tutor, which pays $12 per hour, she earns 12x dollars. If Jackie works y hours as a lifeguard, which pays $9.50 per hour, she earns 9.5y dollars. Thus the total, in dollars, Jackie earns in a week that she works x hours as a tutor and y hours as a lifeguard is 12x + 9.5y. Therefore, the condition that Jackie wants to earn at least $220 is represented by the inequality 12x + 9.5y ≥ 220. The condition that Jackie can work no more than 20 hours per week is represented by the inequality x + y ≤ 20. These two inequalities form the system shown in choice C.
Choice A is incorrect. This system represents the conditions that Jackie earns no more than $220 and works at least 20 hours. Choice B is incorrect. The first inequality in this system represents the condition that Jackie earns no more than $220. Choice D is incorrect. The second inequality in this system represents the condition that Jackie works at least 20 hours.
Which of the following is equivalent to the sum of the expressions a2 − 1 and a + 1 ?
-
Solution
The sum of (a2 − 1) and (a + 1) can be rewritten as (a2 − 1) + (a + 1), or a2 − 1 + a + 1, which is equal to a2 + a + 0. Therefore, the sum of the two expressions is equal to a2 + a.
Choices B and D are incorrect. Since neither of the two expressions has a term with a3, the sum of the two expressions cannot have the term a3 when simplified. Choice C is incorrect. This choice may result from mistakenly adding the terms a2 and a to get 2a2.
In the equation above, k is a constant. If x = 9, what is the value of k ?
-
Solution
If x = 9 in the equation \(\sqrt{K+2}-x=0\), this equation becomes \(\sqrt{K+2}-9=0\),which can be rewritten as \(\sqrt{K+2}=9\). Squaring each side of \(\sqrt{K+2}=9\) gives k + 2 = 81, or k = 79. Substituting k = 79 into the equation \(\sqrt{K+2}-9=0\) confirms this is the correct value for k.
Choices A, B, and C are incorrect because substituting any of these values for k in the equation \(\sqrt{K+2}-9=0\) gives a false statement. For example, if k = 7, the equation becomes \(\sqrt{K+2}-9=\sqrt{9}-9=3-9=0\) which is false.
Which of the following is an example of a function whose graph in the xy-plane has no x-intercepts?
-
Solution
If f is a function of x, then the graph of f in the xy-plane consists of all points (x, f(x)). An x-intercept is where the graph intersects the x-axis; since all points on the x-axis have y-coordinate 0, the graph of f will cross the x-axis at values of x such that f(x) = 0. Therefore, the graph of a function f will have no x-intercepts if and only if f has no real zeros. Likewise, the graph of a quadratic function with no real zeros will have no x-intercepts.
Choice A is incorrect. The graph of a linear function in the xy-plane whose rate of change is not zero is a line with a nonzero slope. The x-axis is a horizontal line and thus has slope 0, so the vgraph of the linear function whose rate of change is not zero is a line that is not parallel to the x-axis. Thus, the graph must intersect the x-axis at some point, and this point is an x-intercept of the graph. Choices B and D are incorrect because the graph of any function with a real zero must have an x-intercept.
What are the solutions of the quadratic equation 4x2 − 8x − 12 = 0?
-
Solution
Dividing both sides of the quadratic equation 4x2 − 8x − 12 = 0 by 4 yields x2 − 2x − 3 = 0. The equation x2− 2x − 3 = 0 can be factored as (x + 1)(x − 3) = 0. This equation is true when x + 1 = 0 or x − 3 = 0. Solving for x gives the solutions to the original quadratic equation: x = −1 and x = 3.
Choices A and C are incorrect because −3 is not a solution of 4x2 − 8x − 12 = 0: 4(−3)2 − 8(−3) −12 = 36 + 24 − 12 ≠ 0. Choice D is incorrect because 1 is not a solution of 4x2 − 8x − 12 = 0: 4(1)2 − 8(1) − 12 = 4 − 8 − 12 ≠ 0.
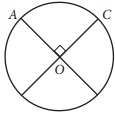
The circle above with center O has a circumference of 36. What is the length of minor arc \(\overset{\frown}{AC}\)?
-
Solution
A circle has 360 degrees of arc. In the circle shown, O is the center of the circle and angle AOC is a central angle of the circle. From the figure, the two diameters that meet to form angle AOC are perpendicular, so the measure of angle AOC is 90°. This central angle intercepts minor arc AC, meaning minor arc AC has 90° of arc. Since the circumference (length) of the entire circle is 36, the length of minor arc AC is \(\frac{90}{360}\times 36=9\).
Choices B, C, and D are incorrect. The perpendicular diameters divide the circumference of the circle into four equal arcs; therefore, minor arc AC is 1⁄4 of the circumference. However, the lengths in choices B and C are, respectively,1⁄3 and 1⁄2 the circumference of the circle, and the length in choice D is the length of the entire circumference. None of these lengths is 1⁄4 the circumference.
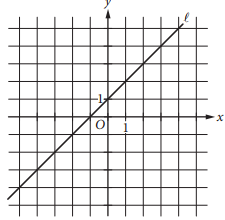
Which of the following is an equation of line A in the xy-plane above?
-
Solution
From the graph, the y-intercept of line is (0, 1). The line also passes through the point (1, 2). Therefore the slope of the line is \(\frac{2-1}{1-0}\) = 1⁄1 = 1⁄1 = 1, and in slope-intercept form, the equation for line l is y = x + 1.
Choice A is incorrect. It is the equation of the vertical line that passes through the point (1, 0). Choice B is incorrect. It is the equation of the horizontal line that passes through the point (0, 1). Choice C is incorrect. The line defined by this equation has y-intercept (0, 0), whereas line l has y-intercept (0, 1).