Note: Figure not drawn to scale.
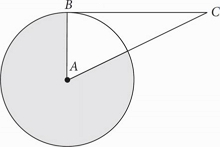
The circle above with center A has an area of 21. BC is tangent to the circle with center A at point B. If AC = 2AB, then what is the area of the shaded region?
-
Solution
The trick is to recognize that ∠ABC is a 30°-60°-90° right triangle.
∠ABC must equal 90° since a tangent line must be perpendicular to the radius of a circle drawn to the point of tangency.
Only a 30°-60°-90° has a hypotenuse (AC) equal to double the length of one of the sides (AB). (You can also use the Pythagorean theorem to show this.)
This means that ∠BAC = 60°, so the shaded region has a central angle measure of 360° - 60° = 300°.
To get the area, use the proportion \(\frac{Central Angle}{360^{\circ}} = \frac{Sector Area}{Circle Area}, \;\; or \;\; \frac{300^{\circ}}{360^{\circ}} = \frac{s}{21}\).
Reduce, cross-multiply, and solve to get s = 17.5. This matches (C).
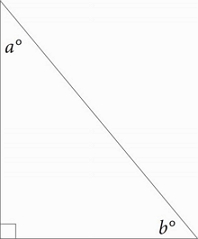
In the figure above, sin a = x. What is the value of cos b?
-
Solution
You can plug in when you're dealing with a geometry problem with unknowns.
When you're Plugging In for a right triangle, use one of the special right triangles to make your life easier.
Use a 3-4-5 right triangle. Make the side opposite a 3, the side adjacent to a 4, and the hypotenuse 5.
Because sine is \(\frac{opposite}{hypotenus}\), sin a = 3⁄5, so x = 3⁄5.
Cosine is \(\frac{adjacent}{hypotenus}\), so cosb = 3⁄5.
This is your target; circle it. Make x = 3⁄5 in each answer choice and look for the answer which equals 3⁄5. Only (A) works.
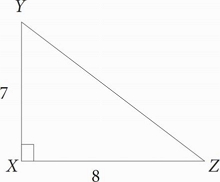
What is the value of tan ∠XZY ?
-
Solution
Tangent is defined as \(\frac{opposite}{adjacent}\).
The side opposite angle XZY is 7, and the side adjacent to this angle is 8, so the tangent of ∠XYZ = 7⁄8 , which is (C).
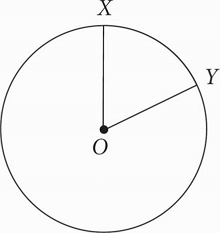
In the figure above, circle O has a radius of 8, and angle XOY measures 5⁄16π radians. What is the measure of minor arc XY ?
-
Solution
Because the question wants arc length and gives you the measure of the central angle in radians, you can use the formula s = rθ to find the arc length:
\(s = \left(8 \right) \left(\frac{5}{16}\pi \right) = \frac{40}{16}\pi\), which reduces to \(\frac{5}{2}\pi\), which is (B).
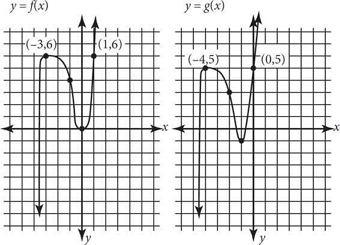
The figures above show the graphs of the functions f and g. The function f is defined by f(x) = 2x3 + 5x2 – x. The function g is defined by g(x) = f(x – h) – k, where h and k are constants. What is the value of hk ?
-
Solution
The second graph moves down 1 and to the left 1.
Remember that when a graph moves to the left, it is represented by (x + h), which would be the same as x - (-1).
So h = -1. Because a negative k represents moving down, k = 1.
Therefore, hk = (-1) × (1) = -1, and the correct answer is (B).
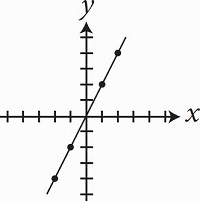
The graph above shows y = 2x. Which of the following graphs represents y = |2x|?
-
Solution
Try plugging in some values for x and see if the graphs include that point.
If x = 0, then y = 0, so (0, 0) should be a point on the graph.
Unfortunately this doesn't eliminate anything.
If x = 1, then y = 2, so (1, 2) should be a point on the graph.
Eliminate (B), (C), and (D).