The mesosphere is the layer of Earth’s atmosphere between 50 kilometers and 85 kilometers above Earth’s surface. At a distance of 50 kilometers from Earth’s surface, the temperature in the mesosphere is −5° Celsius, and at a distance of 80 kilometers from Earth’s surface, the temperature in the mesosphere is −80° Celsius. For every additional 10 kilometers from Earth’s surface, the temperature in the mesosphere decreases by k° Celsius, where k is a constant. What is the value of k ?
-
Solution
The correct answer is 25. In the mesosphere, an increase of 10 kilometers in the distance above Earth results in a decrease in the temperature by k° Celsius where k is a constant. Thus, the temperature in the mesosphere is linearly dependent on the distance above Earth. Using the values provided and the slope formula, one can calculate the unit rate of change for the temperature in the mesosphere to be \(\frac{−80 − (−5)}{80 − 50}=\frac{-75}{30}=\frac{-2.5}{1}\). The slope indicates that, within the mesosphere, if the distance above Earth increases by 1 kilometer, the temperature decreases by 2.5° Celsius. Therefore, if the distance above Earth increases by (1 × 10) = 10 kilometers, the temperature will decrease by ( 2.5 × 10) = 25° Celsius. Thus, the value of k is 25.
−3x + 4y = 20
6x + 3y = 15
If (x, y) is the solution to the system of equations above, what is the value of x ?
-
Solution
The correct answer is 0. Multiplying each side of −3x + 4y = 20 by 2 gives −6x + 8y = 40. Adding each side of −6x + 8y = 40 to the corresponding side of 6x + 3y = 15 gives 11y = 55, or y = 5. Finally, substituting 5 for y in 6x + 3y = 15 gives 6x + 3(5) = 15, or x = 0.
x3 – 5x2 + 2x – 10
For what real value of x is the equation above true?
-
Solution
The correct answer is 5. The four-term polynomial expression can be factored completely, by grouping, as follows:
(x3 − 5x2) + ( 2x − 10) = 0
x2 ( x − 5) + 2 ( x − 5) = 0
( x − 5)( x2 + 2) = 0
By the zero product property, set each factor of the polynomial equal to 0 and solve each resulting equation for x. This gives x = 5 or x = ±i√2, respectively. Because the question asks for the real value of x that satisfies the equation, the correct answer is 5.
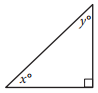
In the triangle above, the sine of x° is 0.6. What is the cosine of y° ?
-
Solution
The correct answer is .6 or 3⁄5. The angles marked x° and y° are acute angles in a right triangle. Thus, they are complementary angles. By the complementary angle relationship between sine and cosine, it follows that sin(x°) = cos(y°). Therefore, the cosine of y° is .6. Either .6 or the equivalent fraction 3⁄5. may be gridded as the correct answer.
Alternatively, since the sine of x° is .6, the ratio of the side opposite the x° angle to the hypotenuse is .6. The side opposite the x° angle is the side adjacent to the y° angle. Thus, the ratio of the side adjacent to the y° angle to the hypotenuse, which is equal to the cosine of y°, is equal to .6.
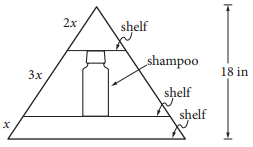
Jim has a triangular shelf system that attaches to his showerhead. The total height of the system is 18 inches, and there are three parallel shelves as shown above. What is the maximum height, in inches, of a shampoo bottle that can stand upright on the middle shelf?
-
Solution
The correct answer is 9. Since the three shelves of the triangular shelf system are parallel, the three triangles in the figure are similar. Since the shelves divide the left side of the largest triangle in the ratio 2 to 3 to 1, the similarity ratios of the triangles are as follows.
⇒ Smallest to middle: 2 to 5
⇒ Smallest to largest: 2 to 6, or 1 to 3
⇒ Middle to largest: 5 to 6
The height of the largest shampoo bottle that can stand upright on the middle shelf is equal to the height of the middle shelf. The height of the entire triangular shelf system is 18 inches. This is the height of the largest triangle.
The height of the middle shelf is the height of the middle triangle minus the height of the smallest triangle. Since the similarity ratio of the middle triangle to the largest triangle is 5 to 6, the height of the middle shelf is 5⁄6(18) = 15 inches. Since the similarity ratio of the smallest triangle to the largest triangle is 1 to 3, the height of the middle shelf is 1⁄3 (18) = 6 inches.Therefore, the height of the middle shelf is 9 inches.
x2 – k⁄2x = 2p
In the quadratic equation above, k and p are constants. What are the solutions for x ?
-
Solution
The given quadratic equation can be rewritten as 2x2 − kx − 4p = 0. Applying the quadratic formula,\(\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}\), to this equation with a = 2, b = −k, and c = −4p gives the solutions \(\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}\).
Choices A, C, and D are incorrect and may be the result of errors in applying the quadratic formula.
If the expression above is rewritten in the form a b + i, where a and b are real numbers, what is the value of a ? (Note: i = √−1 )
-
Solution
To rewrite \(\frac{8-i}{3-2i}\) in the standard form a + bi, multiply the numerator and denominator of \(\frac{8-i}{3-2i}\) by the conjugate, 3 + 2i. This gives \(\left (\frac{8-i}{3-2i} \right )\left ( \frac{3+2i}{3+2i} \right )=\frac{24 + 16i − 3i + (−i)(2i)}{3^{2} − (2i)^{2}}\). Since i1⁄2 = −1, this last fraction can be rewritten as \(\frac{24 + 16i − 3i + 2}{9 − (−4) }=\frac{26 + 13i}{13}\), which simplifies to 2 + i.Therefore, when \(\frac{8-i}{3-2i}\) is rewritten in the standard form a + bi, the value of a is 2.
Choices B, C, and D are incorrect and may be the result of errors in symbolic manipulation. For example, choice B could be the result of mistakenly rewriting \(\frac{8-i}{3-2i}\) as 8⁄3+1⁄2.
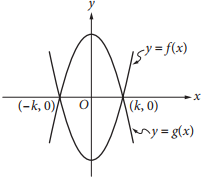
The functions f and g, defined by f(x)=8x2 −2 and g(x) = −8x2+ 2, are graphed in the xy-plane above. The graphs of f and g intersect at the points (k, 0) and (−k, 0). What is the value of k ?
-
Solution
One can find the intersection points of the two graphs by setting the functions f(x) and g(x) equal to one another and then solving for x. This yields 8x2 − 2 = −8x2 + 2. Adding 8x2 and 2 to each side of the equation gives 16x2 = 4. Then dividing each side by 16 gives x2 = 1⁄4, and then taking the square root of each side gives x = ± 1⁄2. From the graph, the value of k is the x-coordinate of the point of intersection on the positive x-axis. Therefore, k = 1⁄2.
Alternatively, since ( k, 0) lies on the graph of both f and g, it follows that f(k) = g(k) = 0. Thus, evaluating f(x) = 8x2 − 2 at x = k gives 0 = 8k2 − 2.Adding 2 to each side yields 2 = 8k2 and then dividing each side by 8 gives 1⁄4 = k2. Taking the square root of each side then gives k = ±1⁄2. From the graph, k is positive, so k = 1⁄2.
Choices A, C, and D are incorrect and may be the result of calculation errors in solving for x or k.
Ken and Paul each ordered a sandwich at a restaurant. The price of Ken’s sandwich was x dollars, and the price of Paul’s sandwich was $1 more than the price of Ken’s sandwich. If Ken and Paul split the cost of the sandwiches evenly and each paid a 20% tip, which of the following expressions represents the amount, in dollars, each of them paid? (Assume there is no sales tax.)
-
Solution
Since the price of Ken’s sandwich was x dollars, and Paul’s sandwich was $1 more, the price of Paul’s sandwich was x + 1 dollars. Thus, the total cost of the sandwiches was 2x + 1 dollars. Since this cost was split evenly, Ken and Paul each paid \(\frac{2x + 1}{2}\) = x + 0.5 dollars plus a 20% tip. After adding the 20% tip, each of them paid (x + 0.5) + 0.2(x + 0.5) = 1.2(x + 0.5) = 1.2x + 0.6 dollars.
Choices A, B, and D are incorrect. These expressions do not model the given context. They may be the result of errors in setting up the expression or of calculation errors.
x = 2y + 5
y = (2x − 3)(x + 9)
How many ordered pairs (x, y) satisfy the system of equations shown above?
-
Solution
Since y = (2x − 3)(x + 9) and x = 2y + 5, it follows that x = 2(( 2x − 3 ) ( x + 9 ) ) + 5 = 4x2 + 30x − 54. This can be rewritten as 4x2 + 29x − 54 = 0. Because the discriminant of this quadratic equation, 292 − (4)(−54) = 292 + 4(54), is positive, this equation has 2 distinct roots. Using each of the roots as the value of x and finding y from the equation x = 2y + 5 gives 2 ordered pairs (x, y) that satisfy the given system of 26 equations. Since no other value of x satisfies 4x2 + 29x − 54 = 0, there are no other ordered pairs that satisfy the given system. Therefore, there are 2 ordered pairs (x, y) that satisfy the given system of equations.
Choices A and B are incorrect and may be the result of either a miscalculation or a conceptual error. Choice D is incorrect because a system of one quadratic equation and one linear equation cannot have infinitely many solutions.