In triangle ABC, the measure of ∠B is 90°, BC = 16, and AC = 20. Triangle DEF is similar to triangle ABC, where vertices D, E, and F correspond to vertices A, B, and C, respectively, and each side of triangle DEF is 1⁄3 the length of the corresponding side of triangle ABC. What is the value of sin F ?
-
Solution
The correct answer is 3⁄5 or .6. Triangle ABC is a right triangle with its right angle at B. Thus,\(\overline{AC}\) is the hypotenuse of right triangle ABC, and \(\overline{BC}\) and \(\overline{BC}\) are the legs of right triangle ABC. By the Pythagorean theorem, AB =\(\overline{BC}\) = 12. Since triangle DEF is similar to triangle ABC, with vertex F corresponding to vertex C, the measure of angle F equals the measure of angle C. Thus, sinF = sinC. From the side lengths of triangle ABC, sinC = \(\frac{pposite\, side}{hypotenuse}=\frac{AB}{AC}=\frac{12}{20}\). Therefore, sinF = 3⁄5.Either 3⁄5 or its decimal equivalent, .6, may be gridded as the correct answer.
At a lunch stand, each hamburger has 50 more calories than each order of fries. If 2 hamburgers and 3 orders of fries have a total of 1700 calories, how many calories does a hamburger have?
-
Solution
The correct answer is 370. A system of equations can be used where h represents the number of calories in a hamburger and f represents the number of calories in an order of fries. The equation 2h + 3f = 1700 represents the fact that 2 hamburgers and 3 orders of fries contain a total of 1700 calories, and the equation h = f + 50 represents the fact that one hamburger contains 50 more calories than an order of fries. Substituting f + 50 for h in 2h + 3f = 1700 gives 2(f + 50) + 3f = 1700. This equation can be solved as follows:
2f + 100 + 3f = 1700
5f + 100 = 1700
5f = 1600
f = 320
The number of calories in an order of fries is 320, so the number of calories in a hamburger is 50 more than 320, or 370.
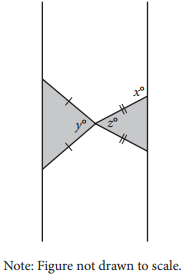
Two isosceles triangles are shown above. If 180 − z= 2y and y = 75, what is the value of x ?
-
Solution
The correct answer is 105. Since 180 − z = 2y and y = 75, it follows that 180 − z = 150, and so z = 30. Thus, each of the base angles of the isosceles triangle on the right has measure \(\frac{180^{\circ} − 30^{\circ}}{2}\)= 75°. Therefore, the measure of the angle marked x° is 180° − 75° = 105°, and so the value of x is 105.
If 7⁄9x − 4⁄9x = 1⁄4 + \(\frac{5}{12}\), what is the value of x ?
-
Solution
The correct answer is 2. First, clear the fractions from the given equation by multiplying each side of the equation by 36 (the least common multiple of 4, 9, and 12). The equation becomes 28x − 16x = 9 + 15. Combining like terms on each side of the equation yields 12x = 24. Finally, dividing both sides of the equation by 12 yields x = 2.
Alternatively, since 7⁄9x − 4⁄9x = 3⁄9x = 1⁄3x and \(\frac{1}{4}+\frac{5}{12}=\frac{3}{12}+\frac{5}{12}=\frac{8}{12}=\frac{2}{3}\), the given equation simplifies to 1⁄3x = 2⁄3. Multiplying each side of 1⁄3x 2⁄3 by 3 yields x = 2.
x3 (x2 − 5) = − 4x
If x > 0, what is one possible solution to the equation above?
-
Solution
The correct answer is either 1 or 2. The given equation can be rewritten as x5 − 5x3 + 4x = 0. Since the polynomial expression on the left has no constant term, it has x as a factor: x(x4 − 5x2 + 4) = 0. The expression in parentheses is a quadratic equation in x2 that can be factored, giving x(x2 − 1)(x2 − 4) = 0. This further factors as x(x − 1)(x + 1)(x − 2)(x + 2) = 0. The solutions for x are x = 0, x = 1, x = −1, x = 2, and x = −2. Since it is given that x > 0, the possible values of x are x = 1 and x = 2. Either 1 or 2 may be gridded as the correct answer.
C = 5⁄9(F − 32)
The equation above shows how a temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true?
I. A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 5⁄9 degree Celsius.
II. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
III. A temperature increase of 5⁄9 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.
-
Solution
If C is graphed against F, the slope of the graph is equal to 5⁄9 degrees Celsius/degrees Fahrenheit, which means that for an increase of 1 degree Fahrenheit, the increase is 9⁄5 of 1 degree Celsius. Thus, statement I is true. This is the equivalent to saying that an increase of 1 degree Celsius is equal to an increase of 9⁄5 degrees Fahrenheit. Since 9⁄5 = 1.8, statement II is true. On the other hand, statement III is not true, since a temperature increase of 9⁄5 degrees Fahrenheit, not 5⁄9 degree Fahrenheit, is equal to a temperature increase of 1 degree Celsius.
Choices A, B, and C are incorrect because each of these choices omits a true statement or includes a false statement.
What are the solutions to 3x2 + 12x + 6 = 0?
-
Solution
Dividing each side of the given equation by 3 givesthe equivalent equation x2 + 4x + 2 = 0. Then using the quadratic formula,\(\frac{−b\pm \sqrt{b^{2-4ac}}}{2a}\), with a = 1, b = 4, and c = 2, gives the solutions x = −2 ± √2.
Choices B, C, and D are incorrect and may be the result of errors when applying the quadratic formula.
The equation \(\frac{24x^{2} + 25x − 47}{ax-2}=-8x-3-\frac{53}{ax-2}\) is true for all values of x ≠ 2⁄a, where a is a constant. What is the value of a ?
-
Solution
Since 24x2 + 25x − 47 divided by ax − 2 is equal to −8x −3 with remainder −53, it is true that (−8x − 3)(ax − 2) − 53 = 24x2 + 25x −47. (This can be seen by multiplying each side of the given equation by ax − 2). This can be rewritten as −8ax2 + 16x − 3ax = 24x2 + 25x − 47. Since the coefficients of the x2 -term have to be equal on both sides of the equation,−8a = 24, or a = −3.
Choices A, C, and D are incorrect and may be the result of either a conceptual misunderstanding or a computational error when trying to solve for the value of a.
y = a(x − 2)(x + 4)
In the quadratic equation above, a is a nonzero constant. The graph of the equation in the xy-plane is a parabola with vertex (c, d). Which of the following is equal to d ?
-
Solution
The parabola with equation y = a(x − 2)(x + 4) crosses the x-axis at the points (−4, 0) and (2, 0). The x-coordinate of the vertex of the parabola is halfway between the x-coordinates of (−4, 0) and (2, 0). Thus, the x-coordinate of the vertex is \(\frac{−4 + 2}{2}\) = −1. This is the value of c. To find the y-coordinate of the vertex, substitute −1 for x in y = a(x − 2)(x + 4): y = a(x − 2)(x + 4) = a(−1 − 2)(−1 + 4) = a(−3)(3) = −9a. Therefore, the value of d is −9a.
Choice B is incorrect because the value of the constant term in the equation is not the y-coordinate of the vertex, unless there were no linear terms in the quadratic. Choice C is incorrect and may be the result of a sign error in finding the x-coordinate of the vertex. Choice D is incorrect because the negative of the coefficient of the linear term in the quadratic is not the y-coordinate of the vertex.

In the figure above, lines k, ℓ , and m intersect at a point. If x + y = u + w, which of the following must be true?
I. x = z
II. y = w
III. z = t
-
Solution
Since the angles marked y° and u° are vertical angles, y = u. Subtracting the sides of y = u from the corresponding sides of x + y = u + w gives x = w. Since the angles marked w° and z° are vertical angles, w = z. Therefore, x = z, and so I must be true.
The equation in II need not be true. For example, if x = w = z = t = 70 and y = u = 40, then all three pairs of vertical angles in the figure have equal measure and the given condition x + y = u + w holds. But it is not true in this case that y is equal to w. Therefore, II need not be true.
Since the top three angles in the figure form a straight angle, it follows that x + y + z = 180. Similarly, w + u + t = 180, and so x + y + z = w + u + t. Subtracting the sides of the given equation x + y = u + w from the corresponding sides of x + y + z = w + u + t gives z = t. Therefore, III must be true. Since only I and III must be true, the correct answer is choice B.
Choices A, C, and D are incorrect because each of these choices includes II, which need not be true.