In the xy-plane, the parabola with equation y = (x − 11)2 intersects the line with equation y = 25 at two points, A and B. What is the length of \(\overline{AB}\)?
-
Solution
Substituting 25 for y in the equation y = (x − 11)2 gives 25 = (x − 11)2. It follows that x − 11 = 5 or x − 11 = −5, so the x-coordinates of the two points of intersection are x = 16 and x = 6, respectively. Since both points of intersection have a y-coordinate of 25, it follows that the two points are (16, 25) and (6, 25). Since these points lie on the horizontal line y = 25, the distance between these points is the positive difference of the x-coordinates: 16 − 6 = 10.
Choices B, C, and D are incorrect and may be the result of an error in solvin the quadratic equation that results when substituting 25 for y in the given quadratic equation.
kx – 3y = 4
4x – 5y = 7
In the system of equations above, k is a constant and x and y are variables. For what value of k will the system of equations have no solution?
-
Solution
If a system of two linear equations has no solution, then the lines represented by the equations in the coordinate plane are parallel. The equation kx − 3y = 4 can be rewritten as y = K⁄3x − 4⁄3, where 4⁄3 is the slope of the line, and the equation 4x − 5y = 7 can be rewritten as y = 4⁄5x − 7⁄5, where 4⁄5 is the slope of the line. If two lines are parallel, then the slopes of the line are equal. Therefore,4⁄5 = k⁄3, or k = \(\frac{12}{5}\) . (Since the y-intercepts of the lines represented by the equations are − 4⁄3 and − 4⁄5, the lines are parallel, not identical.)
Choices B, C, and D are incorrect and may be the result of a computational error when rewriting the equations or solving the equation representing the equality of the slopes for k.
The line y = kx + 4, where k is a constant, is graphed in the xy-plane. If the line contains the point (c, d), where c ≠ 0 and d ≠ 0, what is the slope of the line in terms of c and d ?
-
Solution
The linear equation y = kx + 4 is in slope-intercept form, and so the slope of the line is k. Since the line contains the point (c, d), the coordinates of this point satisfy the equation y = kx + 4: d = kc + 4. Solving this equation for the slope, k, gives k = \(\frac{d-4}{c}\).
Choices B, C, and D are incorrect and may be the result of errors in substituting the coordinates of (c, d) in y = kx + 4 or of errors in solving for k in the resulting equation.
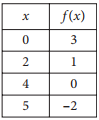
The function f is defined by a polynomial. Some values of x and f(x) are shown in the table above. Which of the following must be a factor of f(x) ?
-
Solution
If x − b is a factor of f(x), then f(b) must equal 0. Based on the table, f(4) = 0. Therefore, x − 4 must be a factor of f(x).
Choice A is incorrect because f(2) ≠ 0; choice B is incorrect because no information is given about the value of f(3), so x − 3 may or may not be a factor of f(x); and choice D is incorrect because f(5) ≠ 0.
2x − 3y = −14
3x − 2y = −6
If (x, y) is a solution to the system of equations above, what is the value of x − y ?
-
Solution
Multiplying each side of the equation 2x − 3y = −14 by 3 gives 6x − 9y = −42. Multiplying each side of the equation 3x − 2y = −6 by 2 gives 6x − 4y = −12. Then, subtracting the sides of 6x − 4y = −12 from the corresponding sides of 6x − 9y = −42 gives −5y = −30. Dividing each side of the equation −5y = −30 by −5 gives y = 6. Finally, substituting 6 for y in 2x − 3y = −14 gives 2x − 3(6) = −14, or x = 2. Therefore, the value of x − y is 2 − 6 = −4.
Alternatively, adding the corresponding sides of 2x − 3y = −14 and 3x − 2y = −6 gives 5x − 5y = −20, from which it follows that x − y = −4.
Choices A, B, and D are incorrect and may be the result of an arithmetic error when solving the system of equations.
If 5⁄x = \(\frac{15}{x+20}\), what is the value of x⁄5?
-
Solution
Multiplying each side of 5⁄x = \(\frac{15}{x+20}\) by x(x + 20) gives 15x = 5(x + 20). Distributing the 5 over the values within the parentheses yields 15x = 5x + 100, and then subtracting 5x from each side gives 10x = 100. Finally, dividing both sides by 10 gives x = 10. Therefore, the value of x⁄5 is \(\frac{10}{5}\) = 2.
Choice A is incorrect because it is the value of x, not x⁄5. Choices B and D are incorrect and may be the result of errors in arithmetic operations on the given equation.
The number of states that joined the United States between 1776 and 1849 is twice the number of states that joined between 1850 and 1900. If 30 states joined the United States between 1776 and 1849 and x states joined between 1850 and 1900, which of the following equations is true?
-
Solution
To fit the scenario described, 30 must be twice as large as x. This can be written as 2x = 30.
Choices A, C, and D are incorrect. These equations do not correctly relate the numbers and variables described in the stem. For example, the expression in choice C states that 30 is half as large as x, not twice as large as x.
Which of the following is equal to a2⁄3, for all values of a ?
-
Solution

If 3r = 18, what is the value of 6r +3 ?
-
Solution
Dividing each side of the equation 3r = 18 by 3 gives r = 6. Substituting 6 for r in the expression 6r + 3 gives 6(6) + 3 = 39. Alternatively, the expression 6r + 3 can be rewritten as 2(3r) + 3. Substituting 18 for 3r in the expression 2(3r) + 3 yields 2(18) + 3 = 36 + 3 = 39.
Choice A is incorrect because 6 is the value of r; however, the question asks for the value of the expression 6r + 3. Choices B and C are incorrect because if 6r + 3 were equal to either of these values, then it would not be possible for 3r to be equal to 18, as stated in the question.
A painter will paint n walls with the same size and shape in a building using a specific brand of paint. The painter’s fee can be calculated by the expression nKℓh, where n is the number of walls, K is a constant with units of dollars per square foot, ℓ is the length of each wall in feet, and h is the height of each wall in feet. If the customer asks the painter to use a more expensive brand of paint, which of the factors in the expression would change?
-
Solution
The painter’s fee is given by nKℓh, where n is the number of walls, K is a constant with units of dollars per square foot, ℓ is the length of each wall in feet, and h is the height of each wall in feet. Examining this equation shows that ℓ and h will be used to determine the area of each wall. The variable n is the number of walls, so n times the area of the walls will give the amount of area that will need to be painted. The only remaining variable is K, which represents the cost per square foot and is determined by the painter’s time and the price of paint. Therefore, K is the only factor that will change if the customer asks for a more expensive brand of paint.
Choice A is incorrect because a more expensive brand of paint would not cause the height of each wall to change. Choice B is incorrect because a more expensive brand of paint would not cause the length of each wall to change. Choice D is incorrect because a more expensive brand of paint would not cause the number of walls to change.
