Which of the following is equivalent to 2x2 – 6x – 8 ?
-
Solution
This question requires factoring the expression 2x2 - 6x - 8.
Begin by factoring 2 from the expression: 2(x2 - 3x - 4).
This expression is further factorable, giving 2(x - 4)(x + 1), which is (A).
If x + y = 0, which of the following must be equivalent to x – y ?
-
Solution
If x + y = 0, then x = -y.
Using this relationship and substituting into the expression x - y, we find that x - y = -y - y = -2y.
This is (A).
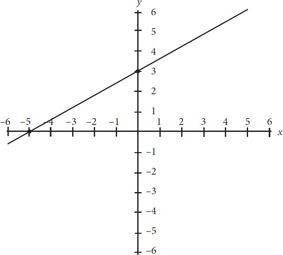
In the figure above, the graph of y = f(x) is shown. Which of the following could be the equation of f(x) ?
-
Solution
The graph of f(x) has a y-intercept at y = 3.
Because of this, we know that when y = 3, x = 0.
f(x) must then satisfy the condition that f(0) = 3. This is true only for (A) and (B).
Alternatively, by recognizing that each equation is in the slope-intercept form: f(x) = y = mx + b, where b is the y-intercept, we can reach the same conclusion.
Next, notice that the slope of the line is positive. That is, as the value of x increases, so too does y.
Returning to the slope-intercept form, m gives the slope of the line.
Only (D) has a positive coefficient (m).
Choice (D), then, is the correct function.
The number of soil samples, s, that Sonal needs for an experiment must be greater than 6 but less than or equal to 13. Which of the following represents an acceptable number of soil samples for Sonal’s experiment?
-
Solution
Sonal needs s soil samples. If according to the question, he must have more than 6 samples, then s > 6.
Also according to the question, he may have no more than 13 samples, so s ≤ 13.
Combining these two expressions, we find that 6 < s ≤ 13. This is (C).
If two times a number is equal to that number minus 4, what is the number?
-
Solution
Translate the question into an equation.
Let x equal the number, and then 2x = x - 4.
Solving for x, we find that x = -4. This is (C).
Which of the following is equivalent to \(\frac{2m + 6}{4} \times \frac{6m – 36}{3m + 9}\)?
-
Solution
Whenever there are variables in the question and answers, think Plugging In.
If m = 2, the expression becomes \(\frac{2\left ( 2 \right ) + 6}{4} \times \frac{6\left ( 2 \right ) - 36}{3\left ( 2 \right ) + 9} = \frac{4 + 6}{4} \times \frac{12 - 36}{6 + 9}\) = \(\frac{-24}{15} = \frac{10}{4} \times \frac{-240}{60} = -4\).
Plug 2 in for m in the answers to see which answer equals the target number of -4.
Choice (A) becomes \(\frac{12\left ( 2 \right )^{2} - 216}{12\left ( 2 \right ) + 36} = \frac{12\left ( 4 \right ) - 216}{24 + 36} = \frac{48 - 216}{60} = \frac{-168}{60} = -2.8\).
This does not match the target number, so eliminate (A).
Choice (B) becomes \(\frac{8\left ( 2 \right ) - 30}{3\left ( 2 \right ) + 13} = \frac{16 - 30}{6 + 13} = \frac{-14}{19}\).
Eliminate (B).
Choice (C) becomes \(\frac{2 - 6}{4} = \frac{-4}{4} = -1\).
Eliminate (C).
Choice (D) becomes m - 6 = 2 - 6 = -4.
The correct answer is (D).

If rectangle ABCD has an area of 324 and the tangent of ∠BCA (not shown) is 4⁄9, then which of the following is closest to the length of BD (not shown)?
-
Solution
First draw lines AC and BD. Now, since tangent is opposite over adjacent, \(\frac{BA}{BC} = \frac{4}{9}\).
Also, BA × BC = 324. Using these two equations as a system of equations can now help get what is needed.
Rearrange the first equation by multiplying both sides by BC to get BA = 4⁄9BC.
Now substitute 4⁄9BC into the first equation to get 4⁄9BC (BC) = 324; this simplifies to 4⁄9BC2 = 324.
Multiply both sides by 9⁄4 to get BC2 = 729, and then take the square root to get BC = 27.
Since the diagonal has to be larger than any of the sides, (A) and (B) are out.
Choice (D) can also be eliminated because our previous calculations can get the length of DC, which is used in the Pythagorean theorem to get BD.
Therefore, the correct answer is (C).
-2y ≤ 8
y – 3 ≤ x
-(1⁄3)y + 1 ≥ x
Which of the following graphs shows the solution to the system of inequalities above?
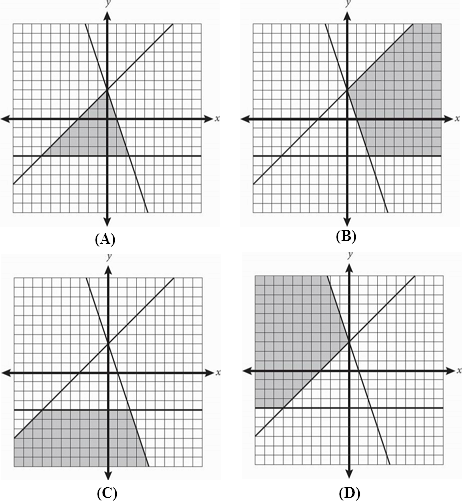
-
Solution
All of the answers have the same lines graphed, so this question is really about the shading.
Plugging In is probably the easiest way to approach this problem.
Start with (0, 0) because this is an easy value to check.
This works in all three equations since 0 ≤ 8, -3 ≤ 0, and 1 ≥ 0.
Therefore, this value needs to be shaded as a possible answer.
Eliminate (B), (C), and (D) because they do not include this point.
The correct answer is (A).
Reactant A is placed in a beaker, to which Reactant B will be added. Reactants A and B will not react unless B gets to a certain concentration. Once the reaction starts, both concentrations decrease until B has been consumed. Which of the following graphs, showing concentration in moles as a function of time in seconds, represents the reaction?
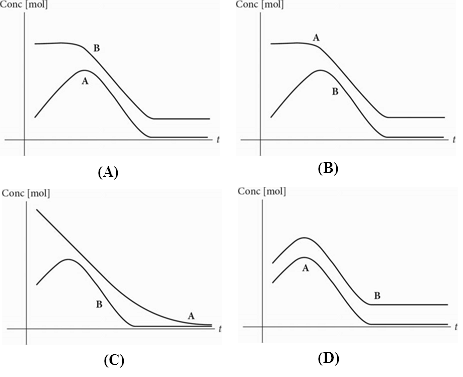
-
Solution
According to the question, Reactant A does not react unless B gets to a certain concentration.
Therefore, the correct answer will have an initial flat line for A while the line for B is rising.
Only graph (B) shows this initial relationship. Therefore, the correct answer is (B).
Which of the following is a possible equation for a circle that is tangent to both the x-axis and the line x = 4 ?
-
Solution
All the answer choices are equal to 4 (which is r2, making r = 2), so you need to focus on where the center of the circle lies.
If the circle is tangent to both the x axis (which is equivalent to the line y = 0) and the line x = 4, then the center must be 2 units from y = 0 and 2 units from x = 4.
Choices (A) and (B) both have centers with an x value of -2 (remember the standard form of the circle equation is (x - h)2 + (y - k)2 = r2, where (h, k) is the center and r is the radius), which is 6 units from x = 4.
Eliminate (A) and (B).
Choice (C) has a center at (2, -4). The x value is 2 units from x = 4; however, the y value is 4 units from y = 0.
Eliminate (C) and choose (D).