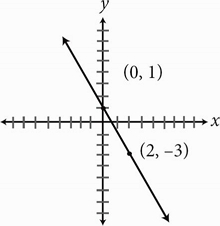
The graph of f(x) is shown in the xy-plane above. Which of the following could be the graph of – [f(x – 2) + 3] ?
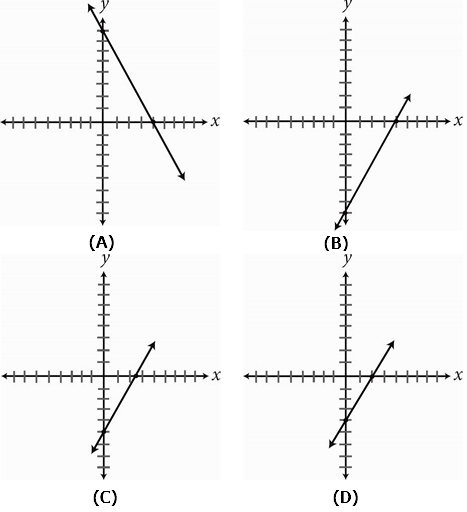
-
Solution
The line shown has a negative slope.
Because the graph transformation asks for the negative value of the transformed function, the resulting graph must have a positive slope.
Therefore, eliminate (A).
Graph transformation rules state that if the number is within the parentheses, then the graph moves left or right in the opposite direction of the sign, and if the number is outside the parentheses, the graph moves up or down in the same direction of the sign.
Therefore, this line will move 2 to the right, and up 3.
To follow the proper order of operations, draw out the graph transformation first, and then deal with the negative outside the brackets.
Move the line two units to the right to get:

Move the line up 3 to get:

The negative sign outside the brackets means to reflect, or flip, the line over the x-axis.
When the line is flipped from a positive to a negative slope, it will still go through point (4, 0).
Therefore, the correct answer is (B).
A 40-foot tall arch with a parabolic shape has a line drawn between the bases of the two legs of the arch. If the height above the ground, y, of the arch can be written as the function y(x) = a(x – 20)(x + 20), where x represents the horizontal distance along the line between the bases from a point on the ground directly under the highest point of the arch, then what is the value of negative constant a ?
-
Solution
When the quadratic is set to 0 the parabola crosses the x-axis at (-20, 0) and (20, 0).
Because parabolas are symmetrical, the vertex of the parabola is at (0, 40).
Plug this point into the equation to get 40 = a(0 - 20)(0 + 20).
Simplify the right side of the equation to get 40 = a(-20)(20) or 40 = -400a.
Solve for a to get \(a = -\frac{40}{400} = -\frac{1}{10}\).
Therefore, the correct answer is (C).
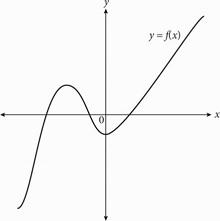
The figure above shows the graph in the xy-plane of the function f. If q, r, s and t are distinct real numbers, which of the following could be f(x) ?
-
Solution
The graph crosses the x-axis at three distinct points.
When the function is set to 0, there should be three real solutions for x.
Use Process of Elimination to solve this question.
Set the equation in (A) to 0 to get 0 = (x - q)2.
In this equation, the root is at x = q, thereby providing only one real value for x. Eliminate (A).
Set the equation in (B) to 0 to get 0 = (x - q)(x + s).
The solutions for this equation are x = q or x = -s.
Therefore, there are only two real solutions for x. Eliminate (B).
Set the equation in (C) to 0 to get 0 = (x - r)(x + s)(x + t).
The solutions for this equation are x = r, x = -s, and x = -t.
Therefore, there are three real solutions for x.
The correct answer is (C).
x + 3y = 42
3x – y = 8
In the system of equations above, how many points of intersection do the equations share and what is their relationship, if any?
-
Solution
First, rewrite the equations so that they are in the slope-intercept form of a line, y = mx + b, where m = slope.
The first equation becomes 3y = -x + 42 or y = -(1⁄3)x + 14.
The slope of this first line is therefore -1⁄3.
The second equation becomes -y = -3x + 8 or y = 3x - 8.
The slope of this line is therefore 3.
The slopes of the two lines are negative reciprocals of each other, which means that the two lines are perpendicular to each other.
The correct answer is (D).

In the figure above, O is the center of the circle and the diameter is 10. If the area of the shaded region is π, what is the length of minor arc XY ?
-
Solution
Since the diameter is 10, the radius must be 5.
A = πr2, so A = 25π. The shaded region takes up \(\frac{\pi}{25 \pi} \; or \; \frac{1}{25}\) of the area, so minor arc XY must take up 1⁄25 of the circumference.
C = πd so C = 10π.
Therefore, the length of minor arc XY is \(\frac{1}{25}\left (10 \pi \right ), \; or \; \frac{2\pi}{5}\), which is (A).
⇒ \(\left ( \frac{3}{c + 2} \right )\left ( c + 2 \right ) = \left ( 5 – \frac{c}{c + 2} \right )\left (c + 2 \right )\)
In the equation above, what is the value of c ?
-
Solution
Plugging In would not be straightforward for this problem, given the fractions and negative numbers.
A better approach would be to simplify the expressions first and then plug in or solve.
Distribute the (c + 2) term to both sides of the equation.
On the left side, this will cancel out with the (c + 2) term in the denominator.
On the right side, make sure to distribute the (c + 2) to both terms inside the parentheses.
The equation becomes \(\frac{3\left ( c + 2 \right )}{c + 2} = \left ( 5\left ( c + 2 \right ) - \frac{c\left ( c + 2 \right )}{c + 2} \right )\) or 3 = 5c + 10 - c.
Combine the c terms and subtract 10 from both sides to get -7 = 4c.
Divide both sides by 4 to find that c = \(-\frac{7}{4}\). The answer is (B).
If the equation for a parabola is y = 5(x – 3)2 – 3, which of the following points represents the parabola’s vertex?
-
Solution
Whenever the question includes variables and the answers are numbers, think Plugging In the Answers.
In (A), x = 3 and y = -3. Plug these numbers into the equation to get -3 = 5(3 - 3)2 - 3.
Solve the right side of the equation to get -3 = 5(0)2 - 3 or -3 = 0 - 3.
The correct answer is (A).
None of the other points work when plugged into the equation, so eliminate (B), (C), and (D).
What is the result of multiplying 8s2 – 6s + 2 by 4s – 1 ?
-
Solution
Whenever there are variables in the question and in the answers, think Plugging In.
If s = 2, the first expression becomes 8(22) - 6(2) + 2 = 8(4) - 12 + 2 = 32 - 12 + 2 = 22.
Therefore, the first expression multiplied by the second expression is 22(7) = 154.
Plug in 2 for s in the answers to see which choice equals the target number of 154.
Choices (A), (B), and (C) yield 26, 70, and 198 respectively.
Choice (D) yields 154 and is the correct answer.
Oil is being drained from an oil tank at a constant linear rate. Four hours after draining of the tank began, the volume of oil in the tank was 740 gallons, and seven hours after draining of the tank began, the volume was 545 gallons. Which of the following functions best models v(t), the volume of oil in the tank, in gallons, t hours after draining of the tank began?
-
Solution
According to the question, if t = 4, then v(t) = 740.
Plug 4 in for t in the answer choices and see if v(t) comes out to the target number 740.
In (A) if t = 4, then v(t) = 740 - 4 = 736. Eliminate (A).
In (B), if t = 4, then v(t) = 740 - 65(4) = 740 - 260 = 480.
Eliminate (B).
In (C), if t = 4, then v(t) = 1,000 - 195(4) = 1,000 - 780 = 220.
Eliminate (C).
The correct answer must therefore be (D).
If A and B both lie on a circle with an area of 16π, and the length of \(\widehat{AB}\) is 2π, what is the radian measure of the central angle between A and B ?
-
Solution
Sketch a picture and write the formulas for arc length and area: s = rθ, A = πr2.
Start by finding the radius.
If the circle has an area of 16π, then 16π = πr2; divide both sides by π to get 16 = r2. The radius must be 4.
So plug in the arc length and radius into your formula: 2π = 4θ.
Divide both sides by 4 to get \(\frac{\pi}{2}\) = θ. Choice (C) is correct.

