4x – (10 – 2x) = c (3x – 5)
If the equation shown has infinitely many solutions, and c is a constant, what is the value of c?
-
Solution
Start by simplifying the left side of the equation.
Don't forget to distribute the negative sign to both terms inside the parentheses.
4x - (10 - 2x) = c(3x - 5)
4x - 10 + 2x = c(3x - 5)
6x - 10 = c(3x - 5)
Next, quickly compare the left side of the equation to the right side.
Rather than distributing the c, notice that if c were 2, then both sides of the equation would equal 6x - 10, and it would have infinitely many solutions.
Therefore, c is 2.
If \(x = k^{-\frac{1}{3}}\) where x > 0 and k > 0, which of the following equations gives k in terms of x?
-
Solution
Raising a quantity to the one-third power is the same as taking its cube root.
Applying a negative exponent to a quantity is the same as writing its reciprocal.
Rewrite the equation using these properties and then solve for k using inverse operations.
Note that the inverse of taking a cube root of a quantity is cubing the quantity.
\(x = k^{-\frac{1}{3}}\)
\(x = \frac{1}{\sqrt[3]{k}}\)
\(\left (x \right )^{3} = \left (\frac{1}{\sqrt[3]{k}} \right )^{3}\)
x3 = 1⁄k
kx3 = 1
k3 = 1⁄x
If g(x) = 3x – 5 and \(h\left (x \right ) = \frac{7x + 10}{4}\), at what point does the graph of g(x) intersect the graph of h(x)?
-
Solution
Two graphs intersect at the point where they have the same x-value and the same y-value.
The notations g(x) and h(x) can both be interpreted as "the y-value at a given value of x," so set g(x) equal to h(x) and solve for x.
Then plug this value into either function to find the corresponding y-value.
Don't let the fraction intimidate you-you can write g(x) as a fraction over 1 and use cross-multiplication.
\(\frac{3x - 5}{1} = \frac{7x + 10}{4}\)
4(3x - 5) = 7x + 10
12x - 20 = 7x + 10
5x = 30
x = 6
g(x) = 3x - 5
g(6) = 3(6) - 5
= 18 - 5
= 13
The graphs of the functions will intersect at (6, 13).
Which of the following are the roots of the equation 2x2 + 4x – 3 = 0?
-
Solution
The equation is already written in the form y = ax2 + bx + c and the coefficients are fairly small, so using the quadratic formula is probably the quickest method.
Jot down the values that you'll need: a = 2, b = 4, and c = -3.
Then, substitute these values into the quadratic formula and simplify:
\(x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}\)
= \(\frac{-\left (4 \right ) \pm \sqrt{\left (4 \right )^{2} - 4\left (2 \right )\left (-3 \right )}}{2\left (2 \right )}\)
= \(\frac{-\left (4 \right ) \pm \sqrt{16 + 24}}{4}\)
= \(\frac{-\left (4 \right ) \pm \sqrt{40}}{4}\)
This is not one of the answer choices, so simplify the radical.
To do this, look for a perfect square that divides into 40 and take its square root.
x = \(\frac{-\left (4 \right ) \pm \sqrt{4 \times 10}}{4}\)
= \(\frac{-\left (4 \right ) \pm 2\sqrt{10}}{4}\)
= \(\frac{-\left (2 \right ) \pm \sqrt{10}}{2}\)
Be careful-you can't simplify the answer any further because you cannot divide the square root of 10 by 2.
If p = 4x3 + x – 2, q = x2 – 1, and r = 3x – 5, then what is 2p – (q + r)?
-
Solution
Break the calculation into steps: Find 2p, find q + r, and then subtract the results.
Arranging the terms in descending order will help keep them organized.
2p = 2(4x3 + x - 2) = 8x3 + 2x - 4
q + r = x2 - 1 + 3x - 5 = x2 + 3x - 6
2p - (q + r) = 8x3 + 2x - 4 - (x2 + 3x - 6)
= 8x3 + 2x - 4 - x2 - 3x + 6
= 8x3 - x2 + 2x - 3x - 4 + 6
= 8x3 - x2 - x + 2
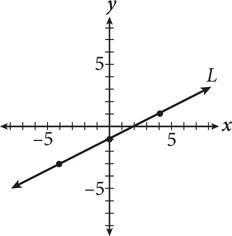
If line L shown here is reflected over the x-axis, what is the slope of the new line?
-
Solution
Line L shown in the graph rises from left to right, so it has a positive slope.
Once reflected over the x-axis, it will fall from left to right, so the new line will have a negative slope.
This means you can eliminate C and D.
Now, draw a quick sketch of the reflected line on the coordinate plane in your test booklet and count the rise (or fall) and the run from one point to the next.

The reflected line falls 2 units and runs 4 units, so the slope is -2⁄4 which reduces to -1⁄2.

Which of the following represents the function shown?
-
Solution
When a quadratic equation is written in vertex form, y = a(x - h)2 + k, the vertex is (h, k).
The vertex of the parabola in the graph is (2, 5); therefore, the equation should look like y = a(x - 2)2 + 5.
This means you can eliminate B and C.
To choose between (A) and D, consider the value of a.
The parabola in the graph opens downward, so a must be negative.
This means (A) is correct.

In the figure shown, ΔABC ∼ ΔDBE. What is the length of \(\overline{BE}\)?
-
Solution
Call the missing side x.
Write a proportion using words first, and then fill in the lengths of the sides that you know:
\(\frac{right \; side \; small \; \bigtriangleup }{base \; of \; small \; \bigtriangleup} = \frac{right \; side \; large \; bigtriangleup}{base \; of \; large \; \bigtriangleup}\)
\(\frac{x}{4} = \frac{2 + x}{6}\)
6x = 4(2 + x)
6x = 8 + 4x
2x = 8
x = 4
The length of \(\overline{BE}\) is 4.
⇒ \(\frac{24x^{4} + 36x^{3} – 12x^{2}}{12x^{2}}\)
Which of the following expressions is equivalent to the expression shown above?
-
Solution
The GCF is 12x2.
\(\frac{24x^{4} + 36x^{3} - 12x^{2}}{12x^{2}}\)
= \(\frac{12x^{2} \left(2x^{2} + 3x - 1 \right)}{12x^{2}}\)
= 2x2 + 3x - 1

The graph shows the cost of installing a vinyl privacy fence. The company charges a flat installation fee plus a cost per linear foot of fencing. Based on the graph, how much does one linear foot of this particular vinyl fence cost?
-
Solution
The cost of one linear foot is the same as the unit rate (the cost per linear foot), which is represented by the slope of the line.
Use the grid-lines and the axis labels to count the rise and the run from the y-intercept of the line (0, 150) to the next point that hits an intersection of two grid-lines.
Pay careful attention to how the grid-lines are marked (by 5s on the x-axis and by 25s on the y-axis).
The line rises 75 units and runs 5 units, so the slope is 75⁄5 = 15 dollars per linear foot of fence.
Note that you could also use the slope formula and two points from the graph to find the unit rate.
