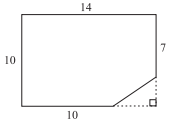
The polygon below was once a rectangle with sides 10 and 14 before a triangle was cut off. What is the perimeter, in inches, of this polygon?
-
Solution
To solve this problem, first determine the length of the unknown side of the polygon. To do so, use the fact that the piece cut off was a right triangle. The unknown side is the hypotenuse of the triangle with legs 14−10 = 4 and 10 − 7 = 3. Use the Pythagorean Theorem to calculate the length of the hypotenuse (the unknown side of the polygon):
42 + 32 = c2
16 + 9 = c2
25 = c2
c = 5The length of the unknown side is 5. Therefore the perimeter of the entire polygon is 14 + 10 + 10 + 7 + 5 = 46.
For a ≠ 0, \(\frac{a^{9}}{a^{3}}\) is equivalent to:
-
Solution
The expression \(\frac{a^{9}}{a^{3}}\) is simplified by subtracting the exponents to get \(\frac{a^{9}}{a^{3}}\) = a9−3 = a6.
If x2 − y2 = 49 and x − y = 7, then x =?
-
Solution
To solve for x, substitute y = x − 7 into the equation x2 − y2 = 49 (Since x − y = 7, y = x − 7):
x2 − (x − 7)2 = 49
x2 − (x2 − 14x + 49) = 49
x2 − x2 + 14x − 49 = 49
14x − 49 = 49
14x = 98
x = 7
Each of the 3 lines crosses the other 2 lines as shown below. Which of the following relationships, involving angle measures (in degrees) must be true?
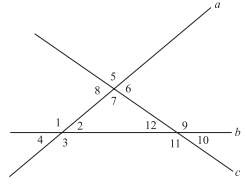
I. m∠2 + m∠7 + m∠12 = 180°
II. m∠4 + m∠5 + m∠10 = 180°
III. m∠3 + m∠8 + m∠11 = 180°
-
Solution
To solve this problem, recognize that any three angles that are part of a triangle add to 180°.
Relationship I: ∠2, ∠7, and ∠12 make up the three angles within the triangle pictured, therefore m∠2 + m∠7 + m∠12 = 180°.
Relationship II: using the property that vertical angles are congruent ∠4 ≅ ∠2, ∠5 ≅ ∠7, and ∠10 ≅ ∠12, therefore m∠4 + m∠5 + m∠10 = 180°.
Relationship III: two of these angles in this relationship are clearly greater than 90° each, thus m∠3 + m∠8 + m∠11 > 180°.
Therefore the only relationships that must be true are I and II.
How many different positive 3-digit integers can be formed if the three digits 3, 4, and 5 must be used in each of the integers?
-
Solution
To easily solve this problem, write out every possible three-digit integer: 345, 354, 435, 453, 534, and 543; six different positive three-digit numbers can be formed.
How many ordered pairs (x, y) of real numbers will satisfy the equation 5x − 7y = 13?
-
Solution
The equation 5x − 7y = 13 defines a line. Since there are an infinite number of points in a line, there are an infi-nite number of ordered pairs (x, y) of real numbers that satisfy the equation 5x − 7y = 13.
In the figure below, what is the sum of p and q?

-
Solution
To solve this problem, set up three other variables, x, y, and z. Let x be the supplement of angle p.
Let y be the supplement of angle q.
Let z be the angle opposite of the 105° angle, so z = 105°. With these new variables, you know that p = 180 − x and q = 180 − y.
This means that p + q = (180 − x) + (180 − y), which simplifies to 360−(x+y). You can see that the three lines form a triangle and that one of the angles is 105°.
That means that the other two angles, x and y must have a sum of 180 − 105, or 75°.
Thus, if x+y = 75°, then p+q = 360−(x+y), or 360−75,which is 285°.
If \(\sqrt{2x}\) + 5 = 9, then x = ?
-
Solution
To solve this problem,first subtract 5 from both sides of \(\sqrt{2x}\) + 5 = 9 to get \(\sqrt{2x}\) = 4. Squaring both sides of \(\sqrt{2x}\) = 4 yields 2x = 16, or x = 8.
One traffic light flashes every 6 seconds. Another traffic light flashes every 9 seconds. If they flash together and you begin counting seconds, how many seconds after they flash together will they next flash together?
-
Solution
To solve this problem, find the least common multiple of 6 and 9. The correct answer is 18 because 6 × 3 = 18 and 9 × 2 = 18.
Which of the following is equal to \(\frac{\left ( \frac{1}{3}-\frac{1}{4} \right )}{\left (\frac{1}{3}+\frac{1}{4} \right )}\)?
-
Solution

