In 3 fair coin tosses, where the 2 outcomes, heads and tails, are equally likely, what is the probability of obtaining exactly 2 heads?
-
Solution
In 3 fair coin tosses, there are exactly 8 equally likely outcomes: HHH, HHT, HTH, HTT, THH, THT, TTH, and TTT. Of these 8 outcomes, 3 include exactly 2 heads, so the probability of obtaining exactly 2 heads is 3⁄8.
How many different integer values of a satisfy the inequality \(\frac{1}{11}\) < 2⁄a < 1⁄8?
-
Solution
You are asked for integer values of a, which means that a must be a whole number. The first step will be to change \(\frac{1}{11}\) to \(\frac{2}{22}\) and 1⁄8 to \(\frac{2}{16}\); now it is easy to see that if 2⁄a is between \(\frac{2}{22}\) and \(\frac{2}{16}\), a can be equal to 21, 20, 19, 18, or 17.
The sum of an infinite geometric sequence series with first term x and common ratio y<1 is given by [latex]\frac{x}{(1 − y)}[/latex]. The sum of a given infinite geometric series is 200, and the common ratio is 0.15. What is the second term of this series?
-
Solution
According to the question stem, the sum of the sequence is given by \(\frac{x}{(1 − y)}\). Therefore, sum = \(\frac{x}{(1 − y)}\). To solve this problem, first substitute the given values into the equation and solve for x:
200 = \(\frac{x}{(1 − 0.15)}\)
200 = \(\frac{x}{0.85}\)
170 = x
The first term of the sequence, x, is 170. To find the value of the second term, multiply 170 by the common ratio, 0.15: 170 × 0.15 = 25.5.
Amy’s best marathon time decreased by 10% from 2005 to 2006 and by 20% from 2006 to 2007. By what percent did her best marathon time decrease from 2005 to 2007?
-
Solution
To solve this problem, let t be Amy’s time in 2005.
Because her time decreased by 10% in 2006, her time in 2006 was (.9)t.
Her time in 2007 would be .8(.9t) = .72t, which means that her time in 2007 was 72% of her time in 2005, so her time decreased by 28%.
In the complex numbers, where i2 = −1,\(\frac{1}{(1 + i)}\times \frac{(1 + i)}{(1 + i)}\) =?
-
Solution

If f (a) = a2 − 2, then f (a + b) =?
-
Solution
To solve this problem, substitute a + b for a in (a2 − 2) as follows:
(a2 − 2)
= (a + b)2 − 2
= (a + b)(a + b) − 2
= a2 + ab + ab + b2 − 2
= a2 + 2ab + b2 − 2
For every positive 2-digit number, a, with units digit x and tens digit y, let b be the 2-digit number formed by reversing the digits of a. Which of the following expressions is equivalent to a − b?
-
Solution
You are given that a is a number with units digit x and tens digit y.
Therefore, x is equivalent to 10 times y, and a = xy = 10x+y.
You are given that b is formed by reversing the digits of a.
Therefore, b = yx = 10y + x.
Set up an equation and solve for a − b as follows:
a − b = (10x + y) − (10y + x)
= 10x + y − 10y − x
= 9x − 9y
= 9(x − y)
If logax = n and logay = p, then loga(xy)2 =?
-
Solution
By definition, loga(xy)2 = 2 loga(xy) = 2(logax + logay).
Because you are given that logax = n and logay = p, the correct answer is 2(n + p).
A 12-centimeter-by-16-centimeter rectangle is inscribed in a circle as shown below. What is the area of the circle, in square centimeters?
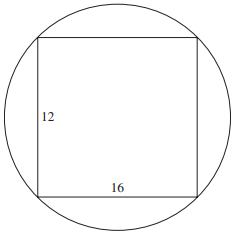
-
Solution
The first step in solving this problem is to calculate the diameter of the circle, which corresponds to the diagonal of the rectangle.
Use the Pythagorean Theorem to determine the length of the diagonal:
122 + 162 = c2
144 + 256 = c2
400 = c2
20 = c
To find the area of the circle, you need the radius, which is equal to one-half the diameter, or 10.
The formula for the area of a circle is A = πr2, so the area is πr2 = 100π.
An integer from 10 through 99, inclusive, is to be chosen at random. What is the probability that the number chosen will have 0 as at least 1 digit?
-
Solution
The first step in solving this problem is to determine how many integers between 10 and 99, inclusive, will have 0 as at least one digit, as follows:
10, 20, 30, 40, 50, 60, 70, 80, 90
There are 9 integers that will have 0 as at least one digit.
Next, because there are a total of 90 numbers in the given range, the probability of choosing one of those 9 numbers is \(\frac{9}{90}\), which simplifies to \(\frac{1}{10}\).
