Points A, B, and C are three different points on a circle, which has area equal to 64π.

Quantity A	Quantity B
AB + AC	32

A. Quantity A is greater
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.

Solution

xy = –60, yz = –50

Quantity A	Quantity B
xz	0

A. Quantity A is greater
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.

Solution

(A) If y is positive, then x and z must both be negative, in order to make the products xy and yz negative. Then xz is the product of two negative numbers and is thus positive and greater than zero. On the other hand, if y is negative, x and z must both be positive in order to make the products xy and yz negative. Then xz is the product of two positives, and again xz > 0, so (A) is greater.

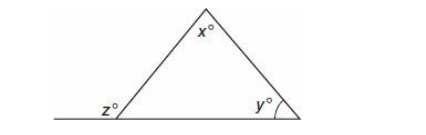
Quantity A	Quantity B
x + y	z

A. Quantity A is greater
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.

Solution

The function f is defined as follows:
f(x) = 3x ⁴ + 5x ² + 7.

Quantity A	Quantity B
f(32)	f(-32)

A. Quantity A is greater
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.

Solution

(C) We can find f(32) for the function f(x) = 3x ⁴ + 5x ² + 7.. by plugging in 32 for x. But this is time-consuming and unnecessary. A negative number raised to an even power is positive, and since x appears only to even powers in f(x), f(–32) must equal f(32). (C).

The circumference of a circle is 2π ²

Quantity A	Quantity B
The area of the circle	27

A. Quantity A is greater
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.

Solution

Sixty stones are placed into four jars in such a way that the ratio of stones in the four jars is 1:2:3:4. What is the least number of stones that can be moved, so that the ratio of stones in the four jars becomes 1:1:1:1?

Solution

(12) Since the ratio is 1:2:3:4, we can think of the jars containing 1x, 2x, 3x, and 4x marbles for some whole number, x. Then 1x + 2x + 3x + 4x = 60, so 10x = 60, and x = 6. This makes the current count of marbles in the jars 1(6), 2(6), 3(6), and 4(6), or 6, 12, 18, and 24. If each jar were to contain 60 ÷ 4 = 15 marbles, the ratio would become 15 : 15 : 15 : 15, which reduces to 1:1:1:1, as required. The minimum number of stones that must be moved to effect this change is 3 + 9 = 12, because three stones moved from the 18 jar to the 12 jar would leave those jars with 15 stones each, and nine stones moved from the 24 jar to the 6 jar would give those jars 15 each.

3 ^x × 3 ^y × 3 ^z = 729. If x, y, and z are three different positive integers and z = x + y, then what is the value of 3 ^z?

Solution

Solution

A builder wants to build a building with the following two properties: each floor has at least one room, each floor has at least twice as many rooms as the floor above it. What is the minimum number of rooms the builder will need for a seven-floor building?

Solution

(127) The minimum occurs when the top floor has one room, and each additional floor has exactly 2 times the number of rooms as the floor above. The total is 1 + 2 + 4 + 8 + 16 + 32 + 64 = 127 rooms.

At a conference, 1/3 of the 900 participants are female, and the rest are male. Of the female participants, 1/4 are retired. Of the male participants, 5/8 are retired. What fraction of all participants at the conference are retired?

A. 1/3
B. 1/2
C. 2/5
D. 3/5
E. 2/3

Solution

(B) There are 1/3 ×900=300 females and, therefore, 900 – 300 = 600 males. For the category of retired individuals, there are 1/4×300=75 retired females, and 5/8 ×600=375 retired males. This means that 75 + 375 = 450 people are retired in all. This represents of all participants, (B)

Which of the following equations has no solutions for x?

A. x ² + 8x = –17
B. x ²+ 8x = –13
C. x ² + 8x = 0
D. x ²+ 8x = 1
E. x ² + 8x = 16

Solution

If \(\frac{21^{60}}{n}\) is a positive integer, which of the following could be n?

A. 2
B. 3
C. 4
D. 5
E 6

Solution

Zoe needs to drive 879 miles in 24 hours. She will need seven rest breaks of a half hour each, during which she will not be driving. Approximately what speed, in miles per hour, will she need to average during the periods when she is driving to finish the journey in time?

A. 40
B 41
C. 42
D. 43
E. 44

Solution

(D) Deduct the time of her rest breaks, 7 × .5 = 3.5 hours, from the 24 hours that she has available. 24 – 3.5 = 20.5 hours. Then her average rate will be the distance traveled, 879 miles, divided by the time spent traveling, 20.5 hours. (879 miles /20.5 hours) = 43 miles/hours = (D)

Solution

A set of test scores at a large university is normally distributed with a mean of 74 and a standard deviation of 7. Which of the following is true?

Indicate all that apply.

A. More students scored above 83 than scored below 63.
B. At least 65% of students scored between 67 and 81.
C. More than half the students scored above 75.

Solution

Line ℓ passes through the points (3, 4) and (6, 5) in the xy-plane. Which of the following could be the equation of a line parallel to line ℓ?
Indicate all such equations.

A. y = 2x + 7
B. y = 3x – 4
C. y = (1/3)x – 5
D. y= (1/3)x + 2
E. y = 3x + 2
F. y = x – 3

Solution

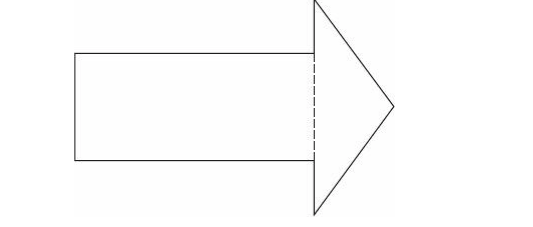
A sign in the shape of an arrow (above) is cut along the dotted line to create a rectangle and a triangle. Which of the following must be true?
Indicate all that apply.
A. The sum of the side lengths of the rectangle is greater than the sum of the side lengths of the triangle.
B. The area of the rectangle is greater than the area of the triangle.
C. The sum of the measures of the angles of the rectangle, in degrees, is greater than the sum of the measures of the angles of the triangle, in degrees.
D. The number of acute angles in the triangle is greater than the number of acute angles in the rectangle.

Solution

Questions are based on the following pie charts, which show the breakdown of 600 participants in a conference by nationality, and the breakdown of the Canadian delegation by occupation (professional field).

How many Canadians from the medical field attended the conference?

A. 32
B. 35
C. 38
D. 40
E. 42

Solution

(E) Canadians make up 20% = .20 = .2 of the 600 total. Of Canadians, 35% are in the medical field. Then there are .35 × .2 × 600 = 42 Canadians in medical, (E)

How many more delegates attended the conference from Brazil than from Tunisia?

Solution

( 48 ) There are 24% – 16% = 8 % more delegates from Brazil than from Tunis ia. 8% of 600 = .08 × 600 = 48.

For all countries other than Canada, an average of 10% of delegates were from the field of education. What percent of all delegates were occupied in the education field?

Solution

(12%) First, calculate that the number of Canadians in education is 20% of 20% of 600, or .2 × .2 × 600 = 24. There are .2 × 600 = 120 Canadian delegates altogether. Of the remaining 600 – 120 = 480 delegates from other nations, 10% are in education, which equals .1 × 480 = 48 delegates. This means that there are 24 (Canadian) + 48 (other nationalities) = 72 delegates from the field of education. This represents 72/600 = .12 = 12%of all participants.

Attempted

0

Correct

0

Wrong

0

Complete