In ABC chemicals, the production of liquid soap rose to 2420 tons from 2000 tons in 2 years. Find the rate of growth per annum.

Solution

The rate of growth can be evaluated by principle of compound interest.

Production after t years = P\(\left ( 1+\frac{R}{100} \right )^{t}\)

∴ 2420 = 2000\(\left ( 1+\frac{R}{100} \right )^{2}\)

∴ \(\left ( 1+\frac{R}{100} \right )^{2}=\frac{121}{100}\)

∴ \(1+\frac{R}{100}=\frac{11}{10}\)

∴ R = 10

∴ Rate of growth is 10% p.a.

In a certain family, eleven times the number of children in the family is greater by 12 than twice the square of the number of children. How many children are there?

Solution

Let x be the number of children.

Then, the equation is 11 x = 2x² + 12

i.e, 2x² - 11 x + 12 = 0

∴ (2x - 3)(x - 4) = 0

∴ x = ³⁄₂ or x = 4

But x has to be a whole number. So x is 4.

In a certain town, 3 people are born every 7 seconds and 7 people die every 11 seconds. Therefore the birth and death rates account for a population growth rate of one person every second.

Solution

3 people are born every 7 seconds. 1 person is born every ⁷⁄₃ seconds. Similarly, one person dies every \(\frac{11}{7}\) seconds.

∴ Net effect = ⁷⁄₃ - \(\frac{11}{7}\) = \(\frac{49 - 33}{21}=\frac{16}{21}\)

∴ Population growth per person will be in \(\frac{16}{21}\) seconds.

17 yellow cubes and 10 blue cubes, all of equal size are fastened together to form one large cube, as shown below

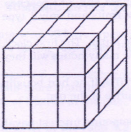
What is the largest fractional part of the surface area of the large cube that could be blue?

Solution

To get maximum surface area-blue, we should place 8 blue cubes at corners. Each corner will show 3 blue faces. Total faces at the corner which are blue will be 24. The remaining 2 blue cubes should be placed on any side next to corners and each cube will show 2 blue faces.

∴ Total blue faces will be 24 + (2 × 2) = 28 out of total small faces 54.

∴ Require fraction =\(\frac{28}{54}=\frac{14}{27}\)

Three typists take 20, 20 and 30 minutes respectively to type the same amount of work. If all 3 work steadily for 5 minutes, what % of the total work does slowest typist turn out?

Solution

The work done by the typists will be in the inverse ratio of their speeds.

∴ Work ratio would be \(\frac{1}{20}:\frac{1}{20}:\frac{1}{30}=\frac{3}{60}:\frac{3}{60}:\frac{2}{60}:3:3:2\)

∴ Slowest typist (i.e. the 3rd typist) will contribute ²⁄₈ = 25%

2 equal sized glasses are respectively ¹⁄₅ and ¹⁄₇ full of apple juice. Then they are filled with milk and contents are mixed in another vessel. The ratio of milk to apple juice in the vessel is

Solution

LCM of 5 and 7 is 35.

Let both the glass have a capacity of 35'upits.

∴ We have

The vessel contains 58 parts of milk and 12 parts of juice.

∴ Required ratio is = 29:6

Paul worked 6 hours in the laboratory and finished ¹⁄₃ of the job. Linda joined him and they finished the job in 4 hours. How long would is it take Linda alone to do the whole job by herself?

Solution

Paul does ¹⁄₃ of the job in 6 hours. ∴ He would finish the complete job in 18 hours.

²⁄₃ of job is done by Paul and Linda in 4 hours.

∴ The complete job Paul and Linda together would take 6 hours. (4 × ³⁄₂)

∴ ¹⁄₆ - \(\frac{1}{18}=\frac{2}{18}\) = (¹⁄₉)^th of the job is done by Linda alone in 1 hour.

∴ She would take 9 hours to do the job by herself

P, Q, R, S are midpoints of sides of square ABCD with area A.

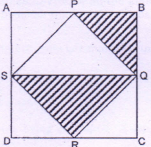
Then the area of shaded region is what fraction of the area of the un-shaded region?

Solution

join all midpoints and we will get 8 equal triangles as shown below. Out of which 3 triangles are shaded.

∴ Answer is ³⁄₅.

The sum of the interior angles of any polygon with n sides is 180(n – 2). If the sum of interior angles of apolygon A = 4 times the sum of exterior angles of pentagon B, how many sides does A have?

Solution

Sum of exterior angles of any polygon = 360°

Sum of all exterior angles of a pentagon = 360°

Sum of all interior angles of polygon A

= 360 x 4 = 1440

∴ 1440 = 180(n - 2) ∴ 8 = n - 2 ∴ n = 10

A vessel full of wine weighs 26 kg. When the vessel is ¹⁄₅ full, it weighs 10 kg. Find the weight of the empty vessel in kg?

Solution

Let the weight of the wine be 'w' kg. and that of empty vessel be 'v' kg.

According to first condition

w + v = 26 ................. (I)

According to second condition

^w⁄₅ + v = 10 ................. (II)

Multiplying equation (II)by 5 and subtracting (I)from it

∴ v = 6 kgs. ∴ The empty vessel weighs 6 kgs

Attempted

0

Correct

0

Wrong

0

Complete

Attempted

Wrong

Correct