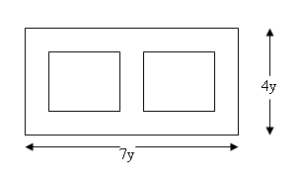
screen-shot-2016-11-07-at-3-49-45-pm

Two square flowerbeds are placed symmetrically in a rectangular garden as shown in the diagram. The distance between the beds is y and so is the width of the border around the beds on all sides. A seed blown into the garden by the wind is equally likely to land anywhere in the garden. What is the probability that it actually lands in a flowerbed?

Solution

Correct Answer: 2/7

Explanation:

The probability is the ratio of the area of the beds to the total area. The sides of the square beds = 4y - 2y = 2y. Area of one bed = 4y². Area of two beds = 8y². Total area is 4y x 7y = 28y². Probability = 8/28 = 2/7

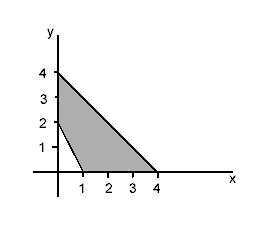
screen-shot-2016-11-07-at-3-49-00-pm

What is the area of the shaded region?

Solution

Correct Answer: 7

Explanation:

The area of the shaded region is the area of the large triangle enclosed between the axes minus the area of the small un-shaded triangle.
8 - 1 = 7

If two lines intersect at a point to form four angles, and one angle is twice as large as its adjacent (neighboring) angle, what is the degree measure of the smallest angle?

Solution

Correct Answer: 60

Explanation:

Let the smallest angle = x
The sum of two vertically opposite angles = 2x
The sum of the other pair of vertically opposite angles = 360 - 2x
But since they are double the measure of angle x their sum also = 4x
Equating gives 360 - 2x = 4x; 360 = 6x; 60 = x
[Or even simpler: the sum of one angle and its neighbor =180. The angles are x and 2x, so 3x = 180 ; x = 60]

A book distributor sends out standardized packages weighing 1, 1.5 or 2 kilograms. If during one week 40 per cent of the packages weigh 1 kg, 50 per cent weigh 1.5 kg and 10 per cent weigh 2 kg, what is the average weight in kilograms of the parcels that week?

Solution

Correct Answer: 1.35

Explanation:

This is a weighted average problem.
The average weight = (40 x 1 + 50 x 1.5 + 10 x 2) 100
(40 + 75 + 20)/100 = 1.35

Different four-letter passwords can be constructed using the letters A, B, C and D only once. How many such passwords exist if either C or B must be in second position?

Solution

Correct Answer: 12

Explanation:

First imagine C in second position. This gives a choice of 1 out of three for first place, and one out of two for third place. This is equivalent to 6 possible combinations.
Now putting B in second place and using the same logic there are 6 more combinations.
Total = 12

A square has sides s and diagonal d. If 2s² + d² = 100, what is the value of s?

Solution

Correct Answer: 5

Explanation:

The diagonal and two sides form an isosceles right triangle.
Using Pythagoras s² + s² = d²; 2s² = d²
Since these terms are equal we can replace d² in the given equation
Hence 2s² + 2s² = 100; 4s² = 100; s² = 25; s = 5

On a map showing only four countries, A, B, C and D, A shares a border with B and C. Country D shares a border with B and C. But countries B and C and countries A and D do not share borders. If the map requires different colours for countries with common borders, what is the minimum number of colours required to complete the map?

Solution

Correct Answer: 2

Explanation:

Draw a diagram.
A and D can be the same color because they do not share a border. Also B and C can be one color, but B and C must differ from A and D. So two colors are needed.

The sum of four consecutive integers is 410. What is the value of the least of these integers?

Solution

Correct Answer: 101

Explanation:

Four consecutive integers can be written n + (n + 1) + (n + 2) + (n + 3)
Their sum = 4n + 6 = 410
4n = 404; n = 101

If 2y – x = 8 , and 3x – y = 1, what is the value of x ?

Solution

Correct Answer: 2

Explanation:

This is a pair of simultaneous equations. Rearrange :
2y - x = 8; -y +3x = 1; multiply the second by 2
-2y + 6x = 2; then add to the first to give
5x = 10; x = 2

A typist can type 45 words per minute. He increases his speed by 20 per cent. How many words can he now type per hour ?

Solution

Correct Answer: 3240

Explanation:

A 20 per cent increase on 45 words per minute = 1.2 x 45 = 54 words per minute.
To get words per hour, multiply by 60 = 3240

Attempted

0

Correct

0

Wrong

0

Complete

Attempted

Wrong

Correct