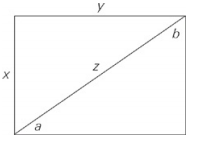
In the rectangle above, a – b > b – a.
| Quantity A | Quantity B |
| z2 – 2x2 | 0 |
-
Solution
Manipulate a – b > b – a to get a > b; hence y, which is the same length as the side across from b, is shorter than x, which is the same length as the side across from a.The diagonal divides the rectangle into two right triangles. According to the Pythagorean theorem, z2 = x2 + y2, so z2 − x2 − y2 = 0 because x > y, x2 > y2. So in Quantity A you are subtracting more than x2 − y2 from z2.Therefore, z2 – 2x2 < 0, so the answer is choice (B).
How much greater, in square inches, is the area of a square with a diagonal of 8 inches than the area of a square with a diagonal of 4 inches?
-
Solution
Draw your own figures.The diagonal of a square creates 45-45-90 triangles with sides in the ratio of x : x : x√2. So, the larger square has a diagonal of x√2 = 8. Divide by √2 to find the side length,\(\frac{8}{\sqrt{2}}\).The area is \(\left (\frac{8}{\sqrt{2}} \right )^{2}\) = 32.The smaller square has a diagonal of x√2 = 4. Divide by √2 to find the side length,\(\frac{4}{\sqrt{2}}\).The area is \((\frac{4}{\sqrt{2}})^{2}\) = 8.The area of the larger square is 32 − 8 = 24 greater than that of the smaller square.
Given four rods of length 1 meter, 3 meters, 5 meters, and 7 meters, how many different triangles can be made using one rod for each side?
-
Solution
According to the Third Side Rule for triangles, the longest side of a triangle must be shorter than the sum of the other two sides. Write out all the possible combinations of sides: 1, 3, 5; 1, 3, 7; 3, 5, 7; 1, 5, 7.The only possible combination of sides that obeys the Third Side Rule is 3, 5, 7.
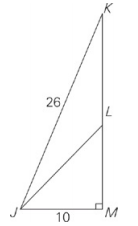
The area of ∆JKL is 65.
| Quantity A | Quantity B |
| KL | LM |
-
Solution
Triangle JKM is the familiar 5-12-13 triple, but doubled, so KM = 24.KL may look the same length as LM, but remember that figures are not drawn to scale. In any triangle, the height is always measured perpendicular to the base from the opposite vertex. So the height of triangle JKL is the length of JM, 10.You are given the area of triangle JKL, so plug all the information you know into the area formula for triangles: A = 1⁄2bb; 65 = 1⁄2(KL)(10);KL = 13. Subtracting KL from KM gives you LM: 24 − 13 = 11; LM = 11. Quantity A is 13, and Quantity B is 11, so the answer is choice (A).
In a triangle, one angle is twice as large as the smallest angle, and another angle is three times as large as the smallest angle. What is the measure of the largest angle?
-
Solution
If x is the measure of the smallest angle, then the other two angle are 2x and 3x.The sum of the angles is 180˚, so x + 2x + 3x = 180. Solve the equation to find x = 30, which means the largest angle measures 90˚.
| Quantity A | Quantity B |
| The length of the side of a square with diagonal \(\sqrt{50}\) | The height of an equilateral triangle with side 6 |
-
Solution
A square cut in half from corner to corner yields two 45-45-90 triangles, so a diagonal of \(\sqrt{50}\)—also known as 5√2—gives a side of 5.The height of an equilateral triangle splits it into two 30-60-90 triangles, so a side of 6 gives a height of 3√3.To compare, express both sides as square roots: 5 is equal to \(\sqrt{25}\), and 3√3 is equal to \(\sqrt{27}\). Quantity B is greater.
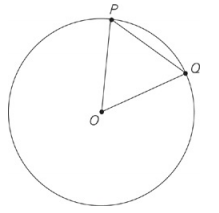
In the Figure above, equilateral triangle OPQ is inscribed in the central angle of the circle and has perimeter 18. What is the area of circle O?
-
Solution
The triangle is equilateral, so dividing the perimeter by 3 gives you the length of 6 for each side. Angle POQ is the central angle of the circle, so sides OP and OQ are also radii of the circle.Thus, the area of the circle is πr2 = π62 = 36π, so the answer is choice (D).
If triangle ABC is equilateral and side AB has a length of s, then what is the area of triangle ABC in terms of s?
-
Solution
First, draw your figure and write out the area formula for triangles,A = 1⁄2bb Then, plug in a number for s; try s = 6. In order to find the height of an equilateral triangle, you need to draw an altitude from the top vertex down the middle to the opposite base, creating two 30-60-90 right triangles.The height of this equilateral triangle is 3√3, so the area formula is 1⁄2 × (6) × (3√3) = 9√3. Now plug 6 in for s in the answer choices.Eliminate choices (C) and (E) because they have the wrong root. Of the remaining answers, only choice (A) yields the target answer of \(9\sqrt{3}:\frac{S^{2}}{4}\sqrt{3}=\frac{36}{4}\sqrt{3}=9\sqrt{3}\)
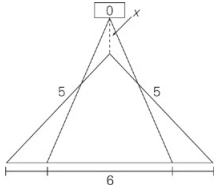
A photographer is using a bipod to steady his camera while taking pictures, as shown in the figure above. The legs of the bipod are 5 feet long and are currently 6 feet apart. If he pulls the legs another 2 feet apart, the top of the bipod drops x feet.
| Quantity A | Quantity B |
| 1 | x |
-
Solution
Split the initial triangle into two right triangles.The figure should look like this:

The smaller triangles are the familiar 3-4-5 triangles, with a height of 4. When the photographer pulls the legs another 2 feet apart, your figure looks like this:

Again, the smaller triangles are 3-4-5 triangles, but now the height is 3. Because x is the change in the triangle’s height, x = 1, so the quantities are equal.
Point A is both in the interior of triangle B and on line C. If A, B, and C are in the same plane, in how many places does line C intersect triangle B?
-
Solution
Draw a triangle with a point inside. Draw a line through the point to see how many places the line intersects with the triangle.There are many ways to draw the line, but each way intersects the triangle at two points.

