A circle of radius 3 is inscribed in a square. What is the product of the perimeter and area of the square?
-
Solution
864
Draw the diagram of the circle in the square, and draw the radii of length 3 from the center straight up and down.This allows you to see that the side of the square is equal to the diameter of the circle and equals 6.The perimeter of the square equals the sum of all the sides, or 24, and the area of the square equals the side squared, or 36. Use your on-screen calculator to find that the product of the
perimeter and the area of the square is 864.
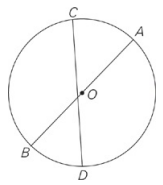
O is the center of the circle above.
| Quantity A | Quantity B |
| Length of line segment AB /td> | Length of line segment CD |
-
Solution
Notice that chord AB goes through the center of the circle.Thus, AB is a diameter; a diameter is the longest chord in a circle.Chord CD does not go through the center of the circle, so AB must be longer than CD.
A circle with center C has a radius of 6.
| Quantity A | Quantity B |
| The ratio of the circumference of C to the radius of C | Half the diameter of C |
-
Solution
For Quantity A, the circumference of C is 2πr = 2π(6) = 12π; the radius is 6. So, the ratio is \(\frac{12\pi }{6}\) = 2π. For Quantity B, half the diameter is the same as the radius, 6.Ballpark that 2π is a little more than 6, making Quantity A greater
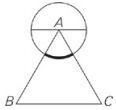
Triangle ABC is equilateral. If the circle with center A has a diameter of 6, what is the length of the darkened arc?
-
Solution
Each angle in an equilateral triangle measures 60°.The degree measure of the darkened arc is therefore 60°, which represents 1⁄6 of the 360° in the circle.Thus, the length of the darkened arc will be 1⁄6 of the circumference of the circle. If the diameter is 6, the radius is 3, so the circumference is 2πr = 6π.1⁄6 of 6π is π.
An office needs to buy circular pizzas for 20 employees. If each pizza is cut into equal slices, and each slice has a central angle of 40°, what is the minimum number of pizzas that need to be ordered so that each employee gets at least two slices of pizza?
-
Solution
5
First, determine the number of slices that will satisfy the question:There are 20 employees that need at least two slices each, so you need a total of at least 40 slices. Next, determine how many slices each pizza has:Each slice has a central angle of 40˚ out of 360˚, so each pizza has \(\frac{360}{40}\) = 9 slices. Since 4 pizzas would only provide 36 slices, you need one more pizza, so 5 is the correct response.
| Quantity A | Quantity B |
| Four times the area of a circular region with a circumference of 4π | The circumference of a circular region with an area of 64π |
-
Solution
For this problem, use the circle formulas—Area = πr2 and Circumference = 2πr—and do the problem one step at a time. For Quantity A, a circle with a circumference of 4π yields 4π = 2πr, so 2r = 4, and r = 2; thus, the area of the circle is 22π, or 4π, and 4 times that is 16π. For Quantity B, a circle with an area of 64π yields 64π = πr2, so r2 = 64, and r = 8; thus, the circumference of the circle is 2(8)π, or 16π.The quantities are equal.
| Quantity A | Quantity B |
| The circumference of a circle with a diameter of 6 | The circumference of a circle with a radius of 12 |
-
Solution
The circumference of a circle with a diameter of 6 is πd = 6π.The circumference of a circle with a radius of 12 is 2πr = 24π, so choice (B) is larger.

Line segments UV, WX, and YZ are diameters of the circles with centers A,B, and C, respectively. If YZ = 2, then what is the area of the circle with center A?
-
Solution
All diameters in a circle are of equal length. Draw a horizontal diameter in the smallest circle; it must be 2 units long.This diameter is also the radius of the circle with center B, whose diameter must therefore be 4 units long. Draw this diameter horizontally, and you realize that it is also the radius of the circle with center A, whose area is πr2 = 16π.
The area of circle C is 9π.
| Quantity A | Quantity B |
| The radius of circle C | 6 |
-
Solution
The formula for the area of a circle is πr2, where r is the radius of the circle. If you set this formula equal to the area of circle C, you get πr2 = 9π. Dividing byπ on both sides of the equation yields r2 = 9, and taking the square root of both sides results in r = 3.The radius of circle C is 3, giving you choice (B) for the answer
What is the degree measure of the smaller angle formed by the hands of a circular clock when it is 10:00?
-
Solution
60
The clock is a circle of 360 degrees, and the 12 numbers create 12 equal intervals around the clock.Therefore, each interval between two consecutive numbers must equal 30 degrees. At 10:00, the two hands are two numbers apart, and create an angle of 60 degrees.
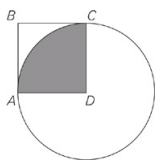
ABCD is a square with side length 2.
| Quantity A | Quantity B |
| The area of the shaded region | π |
-
Solution
The side length of the square is the radius of the circle, so the area of the circle is πr2 = 4π.Central angle CDA measures 90 degrees because ABCD is a square. 90 degrees represents \(\frac{90}{360}=\frac{1}{4}\) of the circle, so the area of the shaded region will be 1⁄4 of the area of the circle,π.The quantities are equal.
Floyd is planting a garden in a triangular plot. One side of the plot measures 5√3, and a second side measures \(7\sqrt{11}\). Which of the following are possible values for the third side of the garden?
Indicate \(\underline{all}\) possible values.
-
Solution
C and D
First calculate values for 5√3 and \(7\sqrt{11}\):The first is approximately 8.66, and the second is approximately 23.22.The third side of a triangle must be greater than the difference of the other two sides and less than the sum of the other two sides; hence, the third side of the garden must measure between 14.56 and 31.88.Calculating for the value of the roots, you will find that only choices (C) and (D) fall within this range.
A parabola follows the function f(x) = x2 – 7x + 3. Point A lies on the parabola at (2, s), and point B lies on the parabola at (6, t). What is the distance from A to B, rounded to the nearest hundredths place?
-
Solution
5.66
Don’t worry if the parabola seems unfamiliar—it’s really just providing you with a way to find the y-values for the given x-values. Plugging 2 in for x gives you –7 for y, so point A is located at (2, –7); using the same process, you can find that point B is located at (6, –3). Plot the two points on a coordinate grid, and make a right triangle by adding a vertex at (2, –3) or (6, –7).Either way, you have a right triangle with short sides of 4√2, so it’s a 45-45-90 triangle, and the long side is . Use your on-screen calculator to determine the final approximate value, 5.66.
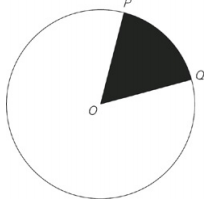
The circle above has center O and circumference 12π. If ∠POQ = 30°, what is the area of the unshaded region?
-
Solution
33π
The formula for the circumference of a circle is circumference = 2πr, so if the circumference is 12π, then the radius must be 6.The formula for the area of a circle is area = πr2 so the area of the circle is 36π. From the question you know that ∠POQ = 30°.The entire circle has 360°, so the shaded region takes up \(\frac{30^{\circ}}{360^{\circ}}=\frac{1}{12}\) of the entire circle.\((36\pi )\times \left ( \frac{1}{12} \right )=3\pi\), so the area of the shaded region is 3π.The shaded area formula is total area – shaded area = unshaded, so you have 36π – 3π = 33π