An interior designer decides to accent a wall with an evenly spaced row of stenciled circles. The wall is 31′6″ long and the stencil has an area of 36π square inches. If the designer wants to leave a space of x inches between each circle and at either end of the row, and x is an integer, then what is the greatest possible number of circles that the designer can use?
-
Solution
29
Draw a rough sketch of the wall, the circles, and the spaces. Notice that there is one space for every circle, plus one more space at the end.The area of each circle is 36π, so r = 6, and the diameter of each circle is 12 inches.Convert the length of the wall into inches: 31 × 12 = 373 inches, plus the extra 6 inches equals 379 inches.You know that the wall in covered in a certain number of circles plus spaces. Let the distance covered by a circle and a space be represented as (12 + x), and the number of circles be represented as y, so now you have y(12 + x) .You also know that there is an extra space, so add an extra x to the end, and this is now the total length of the wall. So, y(12 + x) + 1 = 379 .The question tells us that x must be an integer, and that you need the greatest number of circles, and thus you want x to be as small as possible. Avoid solving the equation and try plugging in 1 for x, since it’s the smallest positive integer. Now the equation becomes y(12 + 1) + 1 = 379, and you can solve for y . So, 13y + 1 = 379 and 13y = 378, leading to y = 29.
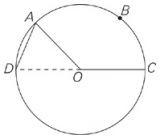
No line segment with endpoints on the circle with center O is longer than line segment DC.
OA = AD = 3
| Quantity A | Quantity B |
| The area of sector OABC | 9 |
-
Solution
Note that OD must be a diameter because it is the longest possible line segment crossing the circle. OA and OD (draw it in) are both radii, and therefore equal in length (3), and both of them are equal to AD.Therefore, triangle OAD is equilateral, and the measure of ∠AOD is 60°.The central angle for sector OABC is 120° (the supplement to 60°), making this sector’s area the area 1⁄3 of the circle:(1⁄2)32π = 3π.Because π is slightly greater than 3, 3π is slightly greater than 9, giving you choice (A) for the answer.
Points A and B lie along the circumference of a circle with center O. A second circle with center M has a radius one-third as long as that of the circle with center O. If the area of sector AOB is equal to the area of the circle with center M, then what is the measure in degrees of ∠AOB?
-
Solution
40
Draw and label the figures, and then set up your scratch paper to Plug In. If circle O has a radius of 6, it has an area of πr2 = 36π; circle M, then, has a radius of 2 and an area of 4π. If sector AOB has an area of 4π out of a total area of 36π, then the sector takes up \(\frac{4\pi }{36\pi }=\frac{1}{9}\) of the entire circle, and ∠AOB represents 1⁄9 of 360°.The correct answer is thus 1⁄9 × 360 = 40.
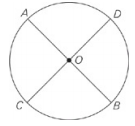
| Quantity A | Quantity B |
| AB + CD | The circumference of the circle with center O |
-
Solution
Plug in a value for the radius of the circle, say r = 2, making the diameter 4;\(\overline{AB}\) and \(\overline{CD}\) are both diameters of the circle, so Quantity A is 8.The circumference of the circle is 4π ≈ 12, so Quantity B is greater.
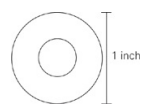
In the figure above, if the area of the smaller circular region is 1⁄2 the area of the larger circular region, then the diameter of the larger circle is how many inches longer than the diameter of the smaller circle?
-
Solution
The diameter of the larger circle, in inches, is 1⁄2, so the radius is .Therefore, the area of the larger circle is \(\pi \left ( \frac{1}{2} \right )^{2}=\frac{\pi }{4}\), and the area of the smaller circle is half this area,π⁄8. Setting this amount equal to the area formula allows you to determine the radius of the smaller circle:πr2 = π⁄8; r = √2⁄4.Therefore, the diameter is √2⁄2. Subtract this amount from 1 (the diameter of the larger circle):\(1-\frac{\sqrt{2}}{2}=\frac{2-\sqrt{2}}{2}\)
The area of Circle A is increased by a factor of x to create Circle B.
The area of Circle B is increased by a factor of x to create Circle C.
| Quantity A | Quantity B |
| The ratio of the radius of Circle A to the radius of Circle C | 1⁄x |
-
Solution
Try plugging in 5 for x. If circle A has an area of 9π, it has a radius of 3.Circle B then has an area of 9π × 5 = 45π.Circle C has an area of 45π × 5 = 225π, with a radius of 15.Therefore, the ratio of circle A’s radius of 3 to circle C’s radius of 15 is 1:5 or 1:x. Alternatively, note that circle C’s area is the area of circle A times x2, making the ratio of the areas 1:x2.The ratio of the radii should be the square root of this ratio, because area is πr2, giving you the ratio 1:x.Both solution methods prove that the quantities are equal.

Line segment AC is tangent to the circle with center O and CO = 5.
| Quantity A | Quantity B |
| Circumference of the circle | 10π |
-
Solution
A tangent to a circle forms a right angle with a radius drawn to the point of tangency. If CO is the hypotenuse of ∆OBC, then you know that the legs of the right triangle must be shorter than 5. Since OB is the radius of the circle, you know that the radius of the circle must be less than 5, so the circumference must be less than 10π.
On a rectangular coordinate plane, a circle centered at (0, 0) is inscribed within a square with adjacent vertices at (0, –2√2) and (2√2,0). What is the area of the region, rounded to the nearest tenth, that is inside the square but outside the circle?
-
Solution
3.4
First, draw and label the figure.Each of the triangles formed by the origin and the two vertices has legs of 2√2 and 2√2. Since each one is an isosceles right triangle—in other words, a 45-45-90 triangle—the sides are in the ratio x:x: x√2, and the long side of each is 2√2 × √2= 4.The long side of a triangle is also the side of the square, so the area of the square is 16. Since the side of the square is the same as the diameter of the circle, the diameter is 4, the radius is 2, and the area of the circle is 4π.The area inside the square but outside the circle, then, is 16 – 4π; use an approximation for π to get 16 – (4 × 3.14) = 3.44.Rounded to the nearest tenth, the answer is 3.4.
If the diameter of circle A is eight times that of circle B, what is the ratio of the area of circle A to the area of circle B?
-
Solution
Plug in 4 for circle B’s diameter; thus circle A’s diameter is 32.The radius of A is 2, and the radius of B is 16; circle B has an area of 4π and circle A has an area of 256π.The ratio is 256π:4π, which reduces to 64:1.

Inscribed square ABCD has a side length of 4. What is the area of the circle?
-
Solution
Draw in either diagonal of the square, which also is the diameter of the circle.You have now created two isosceles right triangles, so the length of the diagonal/diameter is 4√2, and the radius is 2√2.The area of the circle is π(2√2)2= 8π.