The total surface area of a cube is 54.
| Quantity A | Quantity B |
| The length of a diagonal of one face of the cube | 3 |
-
Solution
The surface area of a cube is 6 times the area of each square face of the cube (SA = 6s2), or 54 = 6s2. So each side is 3.The diagonal of the square forms the hypotenuse of a right triangle.Remember that the hypotenuse of a right triangle is always longer than either leg.Therefore, the diagonal is larger than 3.
What is the total surface area of a cube with a volume of 512?
-
Solution
First, write out your formulas and draw a figure.The volume of a cube is V = s3 = 512, giving you s = 8.The surface area of a cube is 6 times the area of each square face of the cube (SA = 6s2), therefore, 6 × 82 = 384.
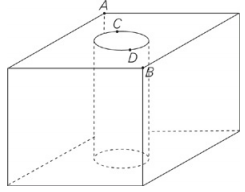
The figure above is a cube with edges of length 9. Points C and D lie on diagonal AB such that points A, C, D, and B are equally spaced. As shown, a right circular cylindrical hole is cut out of the cube so that segment CD is a diameter of the top of the hole. What is the volume of the resulting figure?
-
Solution
You will be subtracting the volume of the cylinder from that of the cube, so the answer will contain π; eliminate choices (A) and (E). To find the volume of the figure, start with the volume of the cube: V= s3 = 93 = 729.The formula for volume of a cylinder is V = πr2h.The cylinder runs the length of the cube, so its height is the same as the length of the cube’s edge, 9. Next, find the radius.The length of diagonal AB is 9√2(remember your special triangles—this is a 45-45-90 triangle!).The points between A and B are equally spaced, so the length of CD, the circle’s diameter, is 1⁄3 the length of AB,3√2.The radius is 1/2 the diameter, or \(\frac{3\sqrt{2}}{2}\). Plug the radius and the height into the formula:\(V=\pi r^{2}b=\pi \left ( \frac{3\sqrt{2}}{2} \right )^{2}(9)=\frac{81\pi }{2}\). Subtract this from the cube’s volume for a final answer of 729 \(729-729-\frac{81\pi }{2}\).
ABCG and CDEF are squares with the same area touching at point C. ∠BCD is a right angle.
| Quantity A | Quantity B |
| 3 times the length of AB | The length of AE |
-
Solution
Draw it! You should end up with two squares oriented the same way touching at C.The squares have the same area, so their sides must be the same length. Plug in a side length for the squares to simplify the comparison—try 2. A square cut in half along its diagonal yields a pair of 45-45-90 triangles, so these two squares with sides of 2 each have diagonals of 2√2. Diagonals AC and CE connect to form segment AE. Quantity A is 3 × 2 = 6, and Quantity B is 2√2 + 2√2 = 4√2 Quantity A is greater.
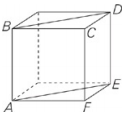
Each edge of the cube shown above has length n. What is the perimeter of quadrilateral ABDE?
-
Solution
Plug in a value for n:Try n = 3. If each edge of the cube is 3, AB = DE = 3, and because the diagonal of a square forms two 45-45-90 triangles,BD = AE = 3√2.The total perimeter is 3 + 3 + 3√2 + 3√2 = 6 + 6√2. Now plug in 3 for n in the answer choices; only choice (A) hits your target.
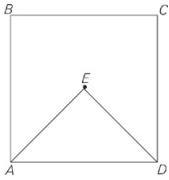
E is the center of square ABCD.
AB = 8
| Quantity A | Quantity B |
| AE | 4 |
-
Solution
The diagonal of a square is always longer than its side, so half a diagonal—segment AE—must be longer than half a side. Half the length of a side of this square is 4.Therefore, AE is larger than 4.
| Quantity A | Quantity B |
| Three times the total surface area of a cube with edge length of 1 centimeter | The total surface area of a cube with edge length of 3 centimeters |
-
Solution
Three times the surface area of a cube with edge length of 1 cm is three times the area of each square face times the number of faces: 3 × (1 cm × 1 cm) × 6 faces = 18 cm2.The surface area of a cube with edge length of 3 cm is (3 cm × 3 cm) × 6 faces = 54 cm2. Quantity B is greater.
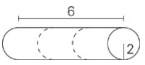
A right circular cylinder with a radius of 2 feet and a length of 6 feet is cut into three equal pieces. What is the volume, in cubic feet,of each of the three pieces?
-
Solution
The answer asks for 1⁄3 of the whole volume, so begin by dividing the height of the trunk by 3 to find the volume of one of the sections of the trunk:\(\frac{6\, ft}{3}\) = 2ft.The volume formula for a cylinder is: V= πr2h = π × 22 × 2= 8π.
A single slice cut from the center of a circular pizza has an edge length (from the center of the pizza to the edge of the crust) of 5″, has an arc length of 1.25π″, and weighs 4 ounces. If a serving weighs 8 ounces, then, to the nearest integer, what is the largest number of servings that six 6″ diameter pizzas can yield? (Note that servings must weigh 8 ounces, but they do not need to be equal in shape.)
-
Solution
The original slice is cut from a pizza with a diameter of 10, and therefore a circumference of 10π.This slice represents \(\frac{1.25\pi }{10\pi }=\frac{1}{8}\) of the circumference and therefore 1⁄8 of the area,\(\frac{25\pi }{8}\) which weighs 4 ounces. A serving weighs 8 ounces, which covers double the area,\(\frac{25\pi }{8}\).The area of the six pizzas is (6)π32 = 54π. Dividing this by the area of one serving gives you the total number of servings that the six pizzas represent:\(\frac{54\pi }{\left ( \frac{25\pi }{4} \right )}=8\frac{16}{25}=8.64\).The six pizzas yield 8 servings
1⁄r of a circular pizza has been eaten. If the rest of the pizza is divided into m equal slices, then each of these slices is what fraction of the whole pizza?
-
Solution
To solve this one, Plug In for r and m:Try r = 2 and m = 4. If 1⁄2 of the pizza has been eaten, and the remaining is divided into 4 equal slices, then each of those remaining 1⁄2 pieces 1⁄8 is of the whole pizza. Now plug in 2 for r and 4 for m in the answer choices; only choice (B) hits your target answer of 1⁄8.