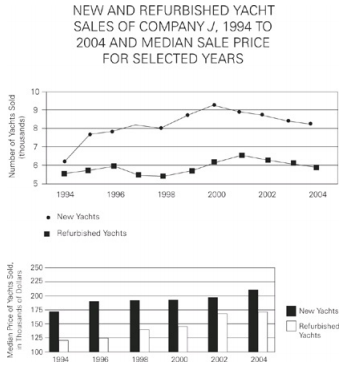
In which of the following years did Company J sell more refurbished yachts than in the previous year, but fewer new yachts than in the previous year?
-
Solution
Because the number of new yachts sold by Company J was always greater than the number of refurbished yachts it sold, a decrease in the former and an increase in the latter results in the two data lines coming closer together. Only the year 2001 shows the correct pattern and both of the proper changes:The number of refurbished yachts sold increased from about 6,200 to about 6,500, and the number of new yachts sold decreased from about 9,300 to about 8,800.The answer is choice (D).

According to the graph, which of the following could be the number of refurbished yachts sold in 1996?
-
Solution
Be sure you’ve identified the correct chart, the correct year, and the correct data line: Use the chart showing the number of yachts sold, the data line showing refurbished yachts, and the information for 1996.The data point for 1996 lies just below 6,000, so select choice (B). If you selected choice (A), you may have used the data line showing information for new yachts; if you selected choice (C), (D), or (E), you may have used information from the wrong year.
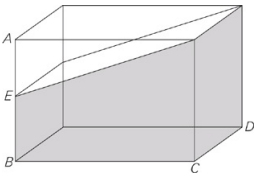
In the rectangular solid depicted above, AB = 6,BC = 8,CD = 5, and AE > EB > 2. Which of the following could be possible values for the volume of the shaded area?
-
Solution
First, find the volume of the entire box, which equals 6 × 8 × 5 = 240. Solve for the volume of the three-dimensional triangular shape on top and subtract it from the total volume to find the volume of the shaded part.The triangular shape has known dimensions of 8 by 5.The third dimension ranges based on the length of AE, with 3 < AE < 4 because AE has to be bigger than EB.Therefore, the triangular shape’s volume falls between one-half of 8 × 5 × 3 = 60 and one-half of 8 × 5 × 4 = 80.The shaded area’s volume falls between 240 – 80 = 160 and 240 – 60 = 180. Only choice (D) works.
A cylindrical object has a volume of 332.75π cubic inches, and its height is equal to its diameter. What is the radius of the object?
-
Solution
5.5
The volume of a cylinder = πr2h. Since the height equals the diameter: 332.75π = π(r2)(2r). Solving for r gives you 5.5 as the final answer

-
Solution
The distance from C to F is the diagonal of the box, so use the Super Pythagorean theorem: a2 + b2 + c2 = d2, where a, b, and c are the sides of the box and d is the diagonal.You have the length and height of the box, so use the volume formula to find the width:720 = (15)(6)w, so the width is 8. Now plug your numbers into the formula: 152 + 82 + 62 = d2, so 325 = d2, and d = 18.03.
If the volume of a cube is 125, then the total area of 2 of its faces is
-
Solution
The volume formula for a cube is V = s3, so a volume of 125 yields a side of 5. One face therefore has an area of 25, and the total area of 2 faces is 50. If you selected choice (C), you may have found the perimeter rather than the area. If you selected choice (B), you may have forgotten to find the total for 2 faces, and if you selected choice (A), you may have done both.
What is the surface area, in square inches, of a box that measures 29 inches by 37 inches by 47 inches?
-
Solution
4,175
Calculate the surface area of each side of the box.Two sides are each: 29 × 37 × 2 = 1,073 square inches.Two other sides are 29 × 47 × 2 = 1,363 square inches.The last two sides are 37 × 47 × 2 = 1,739 square inches.The sum of the six sides is 4,175.
A rectangular shipping container has dimensions of 23 feet by 29 feet by 37 feet. What is the longest distance between any two corners of the container, rounded to the nearest foot?
-
Solution
Draw a rectangular box.The longest distance between any two corners is going to be the box’s three-dimensional diagonal from a bottom corner to the top corner furthest away.You can solve this problem by using the Super Pythagorean theorem a2 + b2 + c2 = d2. 232 + 292 + 372 = 2,739 = d2.The square root is a little more than 52.
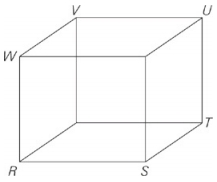
In the rectangular solid above,RS = ST = TU = 7.5. Which of the following is true?
-
Solution
Because all the edges are equal, the figure is a cube.The formula for the surface area of a cube is 6s2, where s is a side of the cube. Thus, the surface area of the solid is 337.5; eliminate choice (A).The formula for the volume of a cube is s3, so the volume of the cube is 421.875; eliminate choice (B). WT is a diagonal of the cube.The formula for the diagonal of a box is a2 + b2 + c2 = d2, where a, b, and c are the sides of the box and d is the diagonal.Thus, WT is 12.99 and does not equal UT.Eliminate choice (C). VS is also a diagonal of the cube, so its length is 12.99.The only correct answer is choice (D).
Emily must ship a cylinder-shaped gift with a height of 11 inches and a volume of 176π cubic inches. What is the volume, in cubic inches, of the smallest rectangular box which can contain this cylinder?
-
Solution
704
Because the cylinder’s height is 11 and its volume is 176π, and V = πr2h, 176π = π(r2)(11), and r = 4.The diameter of the cylinder is 8.The box will need a length of 8 and a width of 8 to accommodate the base of the cylinder, and a height of 11.The volume of the smallest box will equal 8 × 8 × 11, or 704.