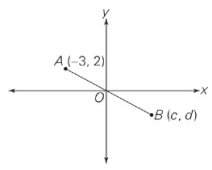
Line AB passes through the origin. If 2 < c < 10, which of the following could be possible values for d ? Indicate all possible values.
-
Solution
C, D, and E
First, find the slope of the line, which runs through (–3, 2) and (0, 0).The slope is the change in y over the change in x, or -2⁄3. Therefore, the equation of line AB is y = -2⁄3x.To find the range of possible values for d, plug in the given range of possible values for c to the equation. If c = 2, d = -4⁄3, and if c = 10, d =-\(\frac{20}{3}\). Any value between -4⁄3 and -\(\frac{20}{3}\) , or –1.33 and –6.67, will work for d.Therefore, the only right answers are choices (C), (D), and (E).

In the coordinate system above, line segment ORis rotated clockwise through an angle of 120° to position OS (not shown).
| Quantity A | Quantity B |
| The x-coordinate of point S | √3 |
-
Solution
Drawing a horizontal line from point R to the positive y-axis forms a right triangle.The length of the leg that sits on the y-axis is √3, and the horizontal leg you just drew has length 1.The ratio of the legs is 1 to √3, so you have a 30-60-90 right triangle.Therefore, the hypotenuse (OR) has length 2, and the angle between OR and the positive y-axis is 30 degrees.The first quadrant includes 90 degrees total, so rotating OR 120 degrees clockwise puts OS on the positive x-axis, with a length of 2.Therefore, the x-coordinate of OS is 2, which is slightly larger than √3, which is approximately 1.7.The answer is choice (A).
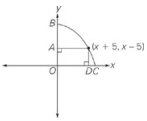
In the figure above, if BC is an arc in the circle with center O, then AB − DC =
-
Solution
To find AB, find the radius of the circle and then subtract OA. If the radius is r, then AB = r − (x − 5) = r − x + 5. Similarly, DC = r − (x + 5) = r − x − 5. So AB − DC = [r − x + 5] − [r − x − 5] = 10, so the answer is choice (B). If you use POE, you can eliminate choice (A) because you know the answer has to be positive. If you selected choice (E), you selected the radius.
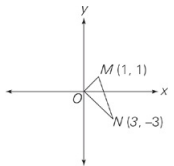
What is the area of triangle MNO in the figure above?
-
Solution
The slope of MO is 1, so it makes a 45 degree angle with the positive x-axis. Similarly, the slope of NO is –1, so it makes another 45 degree angle with the positive x-axis.The sum of the degree measures of these angles is 90, so MNO is a right triangle.Therefore, MO and NO are the base and height of triangle MNO.To find the area of the triangle, you need to find the length of MO and NO. Drop a perpendicular from point M to the y-axis, to form an isosceles right triangle whose hypotenuse is MO.Each leg of this triangle has length 1 so, MO= √2. Similarly, dropping a perpendicular line from the y-axis to point N creates another isosceles right triangle, whose legs have length 3, and whose hypotenuse is NO.Therefore, NO=3√2. So the area of triangle MNO is 1⁄2bh=1⁄2(√2)(3√2)=3, and the answer is choice (A).
Point Z (not shown) lies inside the circle with center P and radius 2 (also not shown).
| Quantity A | Quantity B |
| The x-coordinate of point Z | The y-coordinate of point Z |
-
Solution
Plug in points. Points (3, 4) and (5, 4) both lie inside the circle, so different values give different outcomes.
In the rectangular coordinate plane, the coordinates of points A,B, and C are (1, 4), (7, 4 + 6√3)and (7, 4), respectively. What is the absolute value of the difference between AB and BC ?
-
Solution
Draw the points and connect the points to form a right triangle. Subtract the x-coordinate of A from that of C to find the length of AC: 7 − 1 = 6. Subtract the y-coordinate of C from that of B to find the length of BC: 4+6√3-4=6 . Notice that the ratio of AC to BC is 1 to √3.Therefore, ABC is a 30-60-90 triangle, and the length of AB, the hypotenuse, will be double the length of the shorter side (6), so AB = 12.The absolute value of the difference will be the positive value, obtained by subtracting the smaller value (BC) from the larger value (the length of the hypotenuse, AB): AB – BC=12-6√3, which is choice (E).
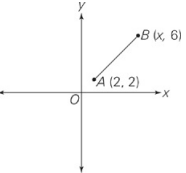
In the coordinate system above, the slope of line segment AB is 4⁄3
| Quantity A | Quantity B |
| The length of line segment AB | x |
-
Solution
Break this one into bite-sized pieces:You need x in order to find the length of AB, so find x first. If you insert the given values into the slope formula, \(\frac{y_{2}-y_{1}}{x_{2}-x_{2}}\), you get \(\frac{y_{2}-y_{1}}{x_{2}-x_{2}}\), so x = 5. Now you need to find the length of AB.Rather than using the distance formula, turn AB into the hypotenuse of a right triangle and find the lengths of the other sides.To make the triangle, add a new vertex at coordinate (5, 2):The length of the horizontal leg is 5 – 2 = 3, and that of the vertical leg is 6 – 2 = 4, yielding the familiar 3-4-5 triangle.The length of segment AB = 5, so the two quantities are equal.
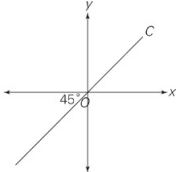
Point D (not shown) lies below line C in the rectangular coordinate system above.
| Quantity A | Quantity B |
| The x-coordinate of point D | The y-coordinate of point D |
-
Solution
Plug in a few points that lie below line c, such as (0, –1), (–3, –4), (1, 0). In each case, the x-coordinate is greater than the y-coordinate, so Quantity A is greater. Alternatively, realize that the 45 degree angle and the fact that the line passes through the origin tells us that the equation of line c is y = x. So the region below the line is the graph of y < x.The coordinates of all points in that region must satisfy the inequality.
If the x-coordinates of the two x-intercepts of a parabola are 3–√2 and 5+√2, then what is the distance between them?
-
Solution
You don’t need to use the distance formula, because the distance between the points (3–√2,0) and (5+√2,0) can be measured horizontally. Distance is positive, so subtract the smaller x-coordinate from the larger: (5+√2)–(3–√2)=2+2 ; the answer is choice (B).
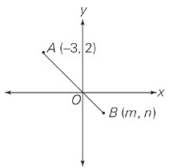
| Quantity A | Quantity B |
| −m | n |
-
Solution
Just because you don’t know the values of –m and n doesn’t mean you can’t determine which is greater. Using point A and the origin, you can find the slope of segment AB:\(\frac{rise}{run}=\frac{-2}{3}=-\frac{2}{3}\). Now plug in coordinates for point B that will give you the same slope; the easiest way to pick them would be to simply rise –2 and run 3, bringing you to the point (m, n) = (3, –2). So –m = –3, and n = –2, and Quantity B is greater