
In the figure above, if a = g, which of the following must be true?
Indicate all possible values.
-
Solution
A, D, F, and G
Plug in for a. If a = 40, then b = 140, g = 40, and h = 140. Now plug in for c. If c = 100, then d = 80, i = 100, and j = 80.You know that g, j, and f must add up to 180, so 40 + 80 + f = 180, which means that f = 60, which in turn means that e = 60. Now check your answer choices to see which ones are true. In this case e = f, so keep choice (A). However, i≠d, so you can eliminate choice (B), and choice (C) is also not true and should be eliminated. 100 + 80 = 180, so you cannot eliminate choice (D). 100 + 140 ≠ 180, so choice (E) is incorrect. 40 + 80 + 60 = 180, so keep choice (F) for now.You have three answers and since this is a must be true question, you should try another set of numbers and test the three choices with the new values to see if the choices are still correct.Choices (A), (D), (F), and (G) are the correct answers.
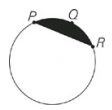
In the figure above, the circumference of the circle is equal to 8π, and arc PQR is equal to 1⁄4 of the total circumference. What is the approximate area of the shaded region? (Round your answer to the nearest whole number.)
-
Solution
4
From the information in the problem you know that 8π = 2πr and r = 4.The area of the circle is equal to πr2, so the area of the circle is 16π. If you draw one radius from the center O of the circle to point P, and another radius from O to point R, you know that the central angle formed will be 90 degrees because arc PQR equals 1⁄4 of the total circle.The triangle formed by inserting these two radii will be an isosceles right triangle with sides of 4, 4, and 4√2 and an area of 8.The total area taken up by the triangle and the shaded area together will be equal to 4π, or 1⁄4 of the circle.The total area – the unshaded area = the shaded area you want, so the shaded area must equal 4π-8.The value of π can be rounded to approximately 3, so now you have 12 – 8 = 4.
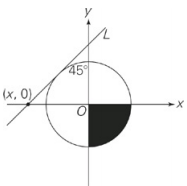
In the figure above, line L is tangent to the circle, which is centered at the origin. The area of the shaded region is equal to the circumference of a circle with radius between 1 and 2(1⁄4). Which of the following could be values of x ?
Indicate all possible values.
-
Solution
D
Use line L to make a triangle, with points at (x, 0), the 45° angle, and the origin.The angle at (x, 0) must be 45° since the sum of the angles of a triangle is 180°. Since line L is tangential to the circle and forms 45° angles with each axis, a line from the point where line L and circle intersect to the origin will form a right angle with line L.The smaller triangle formed—from (x, 0), to where line L and circle meet, to the origin—will be a 45-45-90 triangle, with two sides equal to the radius of the circle. Find the radius of the circle, and you can find x.The area of the shaded region is equal to the circumference of a circle with radius between 1 and 2(1⁄4). Circumference = 2πr, so the area of the shaded region is between 2π and 4.5π, which means the area of the circle in the figure is between 8π and 18π. Area = πr2, so the radius of the circle is between √8 and \(\sqrt{18}\), which is to say between 2√2 and 3√2 . 45-45-90 triangles have sides of a-a-√2a, where, in this case, a is between 2√2 and 3√2 . So the hypotenuse of the triangle, from the origin to (x, 0), is between 2√2√2 and 3√2√2, and therefore between 4 and 6, so x can range from –4 to –6.

If point A is at (0, 8), point C is at (6, 0), and the distance from point B to point C is x, what is \(\frac{x}{\sqrt{7}}\) ?
-
Solution
2
You need to find the length of a leg of a triangle.By finding the lengths of the two other sides, you can use the Pythagorean theorem to find the third side.The hypotenuse of the triangle is the radius of the (quarter-) circle, which, since point A is at (0, 8), is 8. Since point C is (6, 0), the other leg is 6. From the Pythagorean theorem, 62 + x2 = 82, so x2 = 28,x = \(\sqrt{28}=\sqrt{4\times 7}=\sqrt{4}\times \sqrt{7}=2\sqrt{7}\) , so \(\frac{x}{\sqrt{7}}\)=2
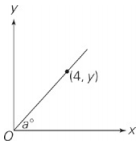
If angle a can range from 45° to 60°, which of the following are possible values for y ?
Indicate all possible values.
-
Solution
C, D and E
Given that the angle ranges from 45° to 60°, you need to plug in values for angle a and find a special triangle to solve for y. If a is 45°, the triangle’s sides are x, x, x . It doesn’t matter what the hypotenuse is; x = 4, which means y also is 4. If a is 60°, the triangle’s sides are x, x , 2x.The shortest side of the triangle would be the one on the x-axis. Since x = 4, then y = 4 = 6.92. So the correct answers range from 4 to 6.92.Choices (C), (D), and (E) are all correct.
The above circle’s circumference includes points (0, 3) and (3, 0), and the base of the inscribed isosceles triangle passes through the center of the circle. What is the area of the triangle?
-
Solution
9
The circle touches (0, 3) and (3, 0), so its center must be at (3, 3) and its radius must be 3. Since the base of triangle passes through the center of the circle, the base of the triangle must be the diameter of length 6. Given the triangle is isosceles and inscribed within the circle, a line from the circle’s center to the triangle’s corner equals the triangle’s height.This height must be the radius of the circle.The area of a triangle is 0.5 × base × height: 0.5 × 6 × 3 = 9.
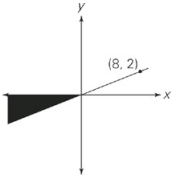
Which of the following points are located in the shaded region of the graph above?
Indicate all possible values.
-
Solution
C and F
First, find the equation of the line that defines the shaded region, expressed as y = mx + b, Using the origin and the one given point in the diagram, the slope m equals 1⁄4, and the y-intercept b is 0. So y = (1⁄4)x is the boundary line. Looking at the figure, if either x or y are positive, then the point isn’t in the shaded region; you can eliminate choices (A), (B), and (E). For the other choices, plug in the x-values. If the resulting y-value is less than the y-value in the choice, that point lies below the line and outside the shaded region. So you’re looking for points for which y ≥ x. when x ≤ (1⁄4)0.This is true for correct choices (C) and (F).