Bob’s typing speed is 60 w.p.m. while Dave’s is 80 w.p.m., and Maria’s is 110 w.p.m. Bob, Dave, Maria charge $4, $5 and $7 per hour respectively. Who is most economical typist if time is not a constraint?

A. Bob
B. Dave
C. Maria
D. Dave and Maria
E. Bob and Dave

Solution

Most economical typist is one who types most number of words per dollar.

Bob's words per dollar =$\frac{60\times 60}{4}$= 900

For Dave it is $\frac{80\times 60}{5}$= 960

For Maria it is $\frac{110\times 60}{7}$ = 943

By mistake instead of dividing $117 among three persons A, B, e in the ratio ¹⁄₂:¹⁄₃:¹⁄₄ it was divided in the ratio 2 : 3 : 4. Who gains most and by how much?

A. A, 28
B. B, 28
C. c, 35
D. c, 25
E. A, 35

Solution

Consider the ratio ¹⁄₂:¹⁄₃:¹⁄₄

LCM of 2,3,4 is 12.

Multiplying all the three ratios by 12, we get 6 : 4 : 3

So A, B, C would have got $54, $36 and $27 respectively.

However they, actually got money in the ratio 2 : 3 : 4 i.e. $26, $39, $52.

So C gains the most i.e. $52 - $27 = $25

Each tree in a forest houses at least one bird. On half the number of trees there are 2 sparrows each. On ¹⁄₄ th of remaining there is one pigeon each, and the rest that housed 4 birds each, are cut for factory use. If there were in all 630 birds in the forest, how many trees were cut?

A. 90
B. 80
C. 120
D. 150
E. 100

Solution

Total Trees are x.

^x⁄₂ trees are 2 sparrows, ∴ total sparrows are x

^x⁄₂ × ¹⁄₄ = ^x⁄₈ trees ave 1 pigeon each.

∴ Total pigeons are ^x⁄₈

Remaining trees are ^x⁄₂ × ³⁄₄ = $\frac{3x}{8}$and they have 4 birds each.

∴ Other birds are $\frac{3x}{8}x4=\frac{3x}{4}$

∴ Total birds are x + ^x⁄₈ + $\frac{3x}{2}$ = 630

∴ x = 240

∴ Total trees cut were $\frac{3x}{8}$ i.e. 90.

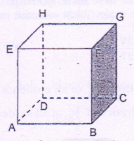
A fly is trapped inside a hollow cube. It moves from A to e along edges of cube, taking shortest possible route. It then comes back to A again along edges, taking longest route (without going over any point more than once}, if the total distance traveled is 5040 meter, what is the area of face of the cube in m2?

A. 99225
B. 32400
C. 396900
D. 216000
E. None

Solution

Side of the cube is x

Shortest route from A to C is AB + BC

Longest route CG + GH + HE + EF + FB + BA

∴Total distance traveled = 8x

8x = 5040 ∴ x = 630

∴ Area of one-face = x² = 396900m²

⁷C₂ + ⁵C₁ + ⁸C₃ – ⁷C₅ – ⁵C₄ – ⁸C₅ = ?

A. 0
B. 1
C. 2
D. 3
E. 4

Solution

ⁿC^r = ⁿC_n- r

∴ ⁷C₂ = ⁷C₅,⁵C₁ = ⁵C₄,⁸C₃= ⁸C₅

Each interior angle of a regular polygon is 11 times its exterior angle: The number of sides of the polygon is

A. 11
B. 18
C. 22
D. 24
E. 12

Solution

An interior angle and corresponding exterior angle of any polygon always add to 1800, as they form a linear pair of angles.

Let exterior angle be x

∴ Interior angle = 11x

∴ 11x + x = 180

∴ x = 15° 11x= 165°

Sum of all exterior angles of any polygon = 360°

$\frac{360}{15}$ = 24 = number of sides of the polygon.

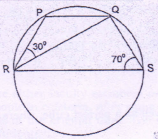
Find ∠PQR where RS=diameter, ∠RSQ = 70°, ∠PRQ = 30°.

A. 40°
B. 50°
C. 45°
D. 55°
E. 60°

Solution

PQRS is a cyclic quadrilateral.

Hence ∠S+ ∠P = 180°

∴ ∠S=70° ∴∠P=110°

∴ ∠PQR = 40°

Find the product of the first five terms, if the third term of G.P. is 4.

A. 64
B. 256
C. 4⁸
D. 1024
E. 4¹⁰

Solution

First term = a

∴ 2^nd term = ar, 3rd term = ar², 4th term = ar³,

5^th term = ar⁴

Product = a⁵ × r¹⁰ = (ar²)⁵

Third term = ar² = 4

∴ Product = 4⁵

Find the sum of the series (5a + 7b) + (8a + 5b) + (11a + 3b) + upto 18 terms.

A. 18a + 18b
B. 549a - 180b
C. 321a + 12b
D. 144a + 152b
E. 549a + 180b

Solution

There are 2 different series

5a + 8a + 11a + to 18 terms

which can be written as 5 + 8 + 11 + etc.

and 7b + 5b + 3b to 18 terms

which can be written as 7 + 5 + 3 etc.

For the first series, first term = 5,

common difference = 3.

For the second series, first term = 7,

common difference = -2.

∴ Sn = ⁿ⁄₂[2a + (n - 1)d]

∴(Sn₁)₁₈ = $\frac{18}{2}$

[2 × 5 + (18 - 1)3]

∴(Sn₁)₁₈ = 9[10 + 17 + 3] = 549

(Sn₂)₁₈ = 2[2 + 7 + 17x(-2)j = 9[14 - 34] = -180

$\frac{a}{2b}=\frac{2}{c}=k$,then$\frac{a+4}{2(b+c)}=$?

A. ¹⁄₂K
B. k²
C. 2k
D. k
E. k + 1

Solution

$\frac{a}{2b}=k$ ∴ a = 2bk

Also $\frac{2}{c}=k\Rightarrow \frac{4}{2c}=k$ ∴ 4 = 2ck

∴$\frac{a+4}{2(b+c)}=\frac{2bk+2ck}{2b+2c}=\frac{k(2b+2c)}{2b+2c}=k$

Attempted

0

Correct

0

Wrong

0

Complete