GRE
Practice Test 20
Previous Solution Next
Linda cuts a 44 em long wire into two parts such that each part is bent into a square with integral sides. Sum of areas of two squares is 73 cm2.
Perimeter of the smaller square Diagonal of the larger suare
  • Solution

    The two squares (with integral values for sides) have areas 9 m2 and 64 m2.

    Perimeter of the smaller square is 12 meters.

    Side of the larger square = 8

    ∴ Diagonal = 8√2

    Col. B is less than 12

(p) equals the greatest integer less than or equal top.
\(\left ( 5\frac{3}{4} \right )+\left ( -4\frac{3}{7} \right )+\left [\left (-2 \frac{3}{5} \right ) \right ]\) 15% of 20
  • Solution

    53⁄4 ⇒ 5

    Similarly \(\left ( -4\frac{3}{7} \right )\) ⇒ -5

    Also \(\left ( -2\frac{3}{5} \right )\) ⇒ -3

    |-3| = 3

    ∴ Col. A = 5 - 5 + 3 = 3

    Col. B = 15% of 20 = 3

a : b = 2 : 5, b : c = 3 : 5
value of c if a is a positive root of a2– 5a – 6 = 0 30
  • Solution

    a2 -5a - 6 = 0 ∴ (a - 6)(a + 1) = O.

    ∴ a = 6 or a = -1

    Since a is positive, a = 6

    ∴ a⁄b = 2⁄5, with a = 6, b = 15

    Also b⁄c= 3⁄5 with b = 15, c = 25

Ten years ago average age of a family of 4 members: Paul, John, Linda and Mary was 22 years. Three children having been born, the average age of family is same today. Two of the children are twins and they differ by two years from the eldest one.
The present age on a twin child 10
  • Solution

    Ten years ago, the total age of 4 family members = 4 × 22 = 88 years.

    Total of the age of these 4 family members today = 88 + (4 × 10) = 128

    Average age of all 7 family members today is also 22 years.

    Hence, total age of all 7 family members today = 7 × 22 = 154

    ∴ Total age of 3 new family members = 154 - 128 = 26 years

    ∴ The age of each child = 8, 8 and 10.

    ∴ Age of a twin child = 8 years.

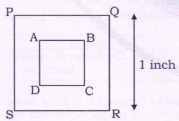
Area of square PQRS is 2 times the area of square ABCD

Diagonal of PQRS – Diagonal of ABCD Diagonal of ABCD
  • Solution

    Let area of PQRS = 4 and ABCD = 2

    Area of square = 1⁄2 d2

    For PQRS 1⁄2d2 = 4 ∴ d = 2√2 = 2.8

    For ABCD 1⁄2d2 = 2 ∴ d = 2

    Col. A = 2.8 - 2 = 0.8

    Col. B = 2

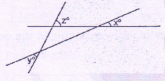
z-x y-x
  • Solution

    x + y +180 - z = 180 ∴ x + y = z ∴ z - x = Y

    Col. A = z - x = x + y - x = y

    Col. B. = y- x

    Since x has to be some positive number, y - x will be less than y.

The relationship between the temperatures on Celsius and Fahrenheit scales is expressed by the equation C = 5⁄9(F-32)where C is temperature in degrees Celsius and F is temperature in degrees Fahrenheit. On a certain day, the temperature increased from 41 degrees to 104 degrees on a Fahrenheit scale.
Increase in the temperature on Celsius scale 33°
  • Solution

    C = 5⁄9 (41 - 32) = 5°

    C = 5⁄9(104 - 32) = 40°

    Increase is 35°

15 men and 18 women together finish a work in 6 days. One man alone finishes that work in 150 days.
Number of days required by 1 woman to finish the job 180
  • Solution

    One man can finish the whole work in 150 days.

    ∴ 1 man does \(\left ( \frac{1}{150} \right )^{th}\) of work in 1 day.

    ∴ 15 men do \(\left ( \frac{15}{150} \right )^{th}\) of work in 1 day.

    ∴ 15 men do \(\left ( \frac{15\times 6}{150} \right )^{th}\)of work in 6 days.

    ∴ \(\frac{15\times 6}{150}=\left ( \frac{3}{5} \right )^{th}\) of work is done by 15 men working for 6 days.

    This implies that (2⁄5)th of work is done ~y 18 women working for 6 days.

    ∴ 1 woman in one day can do \(\frac{2}{5 \times 6 \times 18}\)

    = \(\left ( \frac{1}{270} \right )^{th}\) of the work.

    ∴ One woman can finish the job in 270 days.

 

The least number of complete years in which a sum of money lent at 20% compound interest becomes more than double 5
  • Solution

    ∴ In 4 years sum will be doubled.

Fresh grapes contain 90% water, and dry grapes contain 20% water.
Number of kg. of dry grapes that can be obtained from 20 kg. fresh grapes. 2.4 kg
  • Solution

    Fresh grapes contain 10% pulp, 90% water.

    ∴ 20 kg fresh grapes contain 2 kg. pulp.

    Dry grapes contain 80% pulp and 20% water.

    ∴ With 2 kg. Of pulp, we can obtain

    \(\frac{2}{0.8}\) = 2.5 kg dry grapes.

Attempted

0

Correct

0

Wrong

0

Complete
Quantitative Comparison
Attempted
Wrong
Correct