| Value of \(\frac{pq}{2}\) | 1⁄4 |
-
Solution
(1⁄5)P = √7 ∴ 5- P = 71⁄2
∴ 7 = 5- 2p -I
Also (1⁄7)q = √5 ∴ 7-q = 51⁄2
∴ 7 = 5-1⁄2q -II
From I and II
5-2p = 5-1⁄2q ∴ -2p = -\(\frac{1}{2q}\)
∴ 4pq = 1 ∴ pq⁄2 = 1⁄8
| % increase in the volume of a cube when its edge is doubled | % increase in volume of sphere when its radius is doubled |
-
Solution
Col. A
Let initial edge be a ∴ Volume = a3
Let new edge be 2a ∴ Volume = 8a3
∴ Change in volume = \(\frac{8a^{3}-a^{3}}{a^{3}}\times 100\)
= 700% increase.
Col. B
Let initial radius be r
∴ Volume = 4⁄3πr3
Let the new radius be 2r
∴ New volume = 4⁄3π8r2
= 700% increase.
| |P| | |q| |
-
Solution
Let p and q be positive numbers.
∴ If p > q (e..g., 4 > 3), then |p| > |q|
Let p and q be negative numbers.
(e.g. -3 > -4)
∴ |P| is positive p and |q| is positive q.
∴ |p| < |q|
| K+2 | 10 |
-
Solution
8 × 9 × 10 = 720
∴ K = 7 K + 2 = 9
| \(\frac{2m-\frac{n-5}{6}}{\frac{n-5}{3}4m}\) | -0.5 |
-
Solution
Col. A-
\(\frac{\frac{12m-n+5}{6}}{\frac{n-5-12m}{3}}=\frac{12m-n+5}{2n-10-24m}\)
=-\(\frac{12m-n+5}{24m-2n+10}=\frac{1(12m-n+5)}{2(12m-n+5)}\)
= -1⁄2 = -0.5
Col. B - -0.5
| Probability that atleast one head will be thrown | 1⁄2 |
-
Solution
Col. A-
Events = HH, HT, TH, TT
(H = Head, T = Tail)
∴ Probability = 3⁄4 (At least one head)
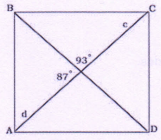
ABCD is rectangle.
| c | d |
-
Solution
Redraw the figure in following manner

Clearly d > c
| w⁄y | x⁄z |
-
Solution
Note that all numbers are positive.
Let w = 4, x = 3, Y = 2, Z = 1
∴ Col. A - Col. B -
w⁄y = 2 x⁄z = 3
∴ Col. B > Col. A
Consider a second set of values
w = 40, x = 14, Y = 2, Z = 1
∴ w⁄y=20 x=\(\frac{14}{1}\)=14
∴ Col. A> Col. B
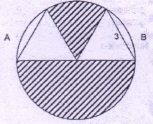
AB is the diameter
Each of the triangles is equilateral
| Area of shaded region | 6π |
-
Solution
Since triangles are equilateral the central angles measure 60° and their sum is 120° So unshaded area 1⁄3 of circle and shaded are 2⁄3 of circle.
∴ Area of shaded region = 2⁄3 × π × (3)3 = 6π
(Shaded region is semicircle + sector of 60 = 2⁄3 of the circle.)
| 4m + 11 | 44 – 6n |
-
Solution
2m = 11 - 3n
Col. A-
4m + 11 = 22 - 6n + 11 = 33 - 6n
Col. B-
Canceling -6n from both sides
