GRE
Practice Test 38
Previous Solution Next
The areas of 3 different sized faces of rectangular solid are 6,8, 12 cm2.
Volume of the solid in cm. 363
  • Solution

    Let a, b, c be the dimensions of the rectangular solid. Then ab = 6, be = 8, ac = 12

    Multiplying all the 3 equations

    (abc)2 = 6 × 8 × 12

    ∴ (abc)2 = 2 × 3 × 2 × 4 × 4 × 3

    ∴ (Volume)2 = (2 × 3 × 4)2

    ∴ Volume = 2 × 3 × 4 = 24 cm3

    ∴ Col. A = 24, Col. B = 36

Sum and difference of the ages of Sam and Winny is 60 years and 4 years respectively.
Winny’s Age 30
  • Solution

    \(\frac{x-y=4}{2x = 64}\)

    X = 32.

    So the other person's age is 28 but we don't know who is Winny.

If both 72 and 53 are the factors of the number a × 7 × 62 × 5 × 11 then
smallest value of a 175
  • Solution

    72 is the factor of this number. :. it should include one more 7. Similarly, it should also include

    5 × 5 = 52 ∴ Smallest value of a = 52 × 7 = 175.

    x + y = 60

x and y are negative integers. If x – y = 1
the least possible value of xy 2
  • Solution

    Smallest value that satisfies the equation are y = -2 and x = -1.

    ∴ xy = 2

3 students Play only Volleyball.
Number of students playing football 53
  • Solution

    z = 3

    ∴ 9 + 11 +3 + x = 36 ∴ x = 13

    ∴ Col. A = Addition of all elements in the third circle = 11 + 13 + 8 + 13 = 45

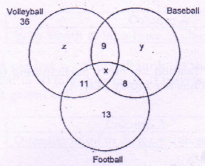
Answer the following question based on the information given in the Venn diagram.

Number of students playing volleyball or football 49
  • Solution

    It is the addition of all elements in the 2 circles pertaining to Volleyball and Football = 36 + 8 + 13 = 57

My cousin had come to my home for vacation. We played one game of chess every day. We played our last match on the day she left. We had decided that whosoever loses has to give one candy to the winner. None of our games ended in a draw. She gave me a total of 11 candies in spite of winning 7 matches and I didn’t give her anything.
Numbers of days she stayed at my place 25
  • Solution

    My cousin won 7 matches, so I owe her 7 candies. However, she gave me 11 finally.

    This means she lost 18 matches and I lost 7 i.e. in all 7 + 18 = 25 games were played.

    ∴ She stayed for 25 days.

Mrs. Smith has 15 children born with a difference of one and half years. Miss Shelly admits that she is the oldest and is 8 times older than Smith Junior who is the youngest.
Age of Miss Shell 24 years
  • Solution

    Difference between the age of the youngest and oldest will be 14 × 1.5 = 21 years.

    If Smith Junior is x years, then Shelly is x + 21 years.

    ∴ x + 21 = 8x :∴ 7x = 21 ∴ x = 3

    ∴ Miss Shelly's age = 3 + 21 = 24 years.

    ∴ Col. A = 24, Col. B = 24

Eva is 20 years older than her son Frank. In 8 years Eva will be twice as old as Frank.
Eva’s present age 36
  • Solution

    Frank's age is x. ∴ Eva's age is x + 20.

    After 8 years Frank's age will be x + 8, Eva's age will be x + 28

    ∴ x + 28 = 2 (x + 8)

    ∴ x + 28 = 2x + 16

    ∴ x = 12

    ∴ Eva's age = 12 + 20 = 32.

    Col. A = 32

72 candies are to be distributed equally among ‘c’ children
Number of different value of ‘c’ 8
  • Solution

    Method 1 :

    'c' can take as many values as the number of factors of 72.

    Let's factorise 72

    72 = (2 × 2 x 2 × 3) × 3

    24 candies x 3 children and vice versa

    72 = (2 × 2 × 2 ) × (3 × 3)

    8 candies × 9 children and vice versa

    72 = (2 × 2 ) × (2 × 3 × 3)

    4 candies x 18 children and vice versa

    72 = 2 ( 2 × 2 × 3 × 3)

    2 candies × 36 children and vice versa

    And also 1 candy each to 72 children.

    ∴ Total values of Care 9.

Attempted

0

Correct

0

Wrong

0

Complete
Quantitative Comparison
Attempted
Wrong
Correct