The figure shows a rectangle inscribed in a circle. The side AB measures 28 em and side BC measures 21 cm. A black ant starts travelling from point A along the circumference of circle at 22 cm/minute. She will complete 7 rounds in x minutes.

A. if the quantity in Column A is greater
B. if the quantity in Column B is greater
C. if the two quantities are equal
D. if the relationship cannot be determined from the information given

Solution

By Pythagoras theorem, diameter AC = 35 cm.

∴ Circumference circle = \(\frac{22}{7}\) × 35 = 110 cm.

∴ Black ant would take \(\frac{110}{22}\) = 5 minutes to complete one round and reach A again.

She will complete 7 rounds in 7 × 5 = 35 min.

∴ x = 35 min

A river flows at 4 kmph. A boat can go downstream thrice as fast as it can go upstream.

Seed of boat in still water in kmph

A. if the quantity in Column A is greater
B. if the quantity in Column B is greater
C. if the two quantities are equal
D. if the relationship cannot be determined from the information given

Solution

Let speed of boat in still water = x kmph.

∴ Upstream speed = x - 4

Downstream speed = x + 4

∴ x + 4 = 3(x - 4) x + 4 = 3x - 12

∴ 2x = 16 ∴ x = 8 ..... Col. B > Col. A

The minute hand of a clock is found to cross the hour hand at ‘t’ minutes past 4.

t	\(20\frac{9}{11}\)

A. if the quantity in Column A is greater
B. if the quantity in Column B is greater
C. if the two quantities are equal
D. if the relationship cannot be determined from the information given

Solution

At 4 o'clock, the difference between hour and minute hand is 20 minutes i.e. minute hand lags the hour hand by 20 minutes. In 60 minutes, minute hand gains 55 minutes over hour hand.

∴ To gain 20 minutes over the hour hand, minute hand must actually show \(\frac{20\times 60}{55}=20\times \frac{12}{11}\)

=\(\frac{240}{11}=21\frac{9}{21}\) minutes past 4.

Col. A > Col. B

Jonty and Lance start travelling in the same direction at 8 kmph and 13 kmph respectively After 10 hours, Jonty doubled his speed and Lance reduced his speed by 1 kmph. and they reached the destination together.

tonal duration of journey in houres

A. if the quantity in Column A is greater
B. if the quantity in Column B is greater
C. if the two quantities are equal
D. if the relationship cannot be determined from the information given

Solution

In 10 hours, lead taken by Lance = (13 - 8) × 10 = 50 km

New speed of Jonty = 16 kmph and that of Lance = 12 kmph

∴ Jonty has to cover 50 Ian with a relative speed of 4 kmph in \(\frac{50}{4}\) = 12¹⁄₂ hours.

∴ Col.A = 10 + 12¹⁄₂ = 22¹⁄₂hours

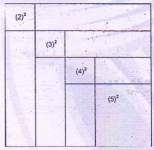
The figure above consists of 4 squares and 6 rectangles. Areas of the 4 squares are as shown.

perimeter of the figure

A. if the quantity in Column A is greater
B. if the quantity in Column B is greater
C. if the two quantities are equal
D. if the relationship cannot be determined from the information given

Solution

Note that the sum of sides of the 4 squares = side of the big square.

∴ Length of square = 2 + 3 + 4 + 5 = 14

∴ Col A = 14 × 4 = 56 > Col. B

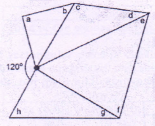
average arithmetic means of the 8 marked angles

75°

A. if the quantity in Column A is greater
B. if the quantity in Column B is greater
C. if the two quantities are equal
D. if the relationship cannot be determined from the information given

Solution

Addition of all 4 triangles = 180 × 4 = 7200

Total of angles around the central point = 360° - 120° = 240°

∴ The average degree measure of 8 angles =\(\frac{480}{8}\)= 60

∴ Col. A < Col. B

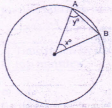
The figure shows a circle with centre O.

20° ≤ x < 50°

Difference between Maximum and Minimum possible value of y°

A. if the quantity in Column A is greater
B. if the quantity in Column B is greater
C. if the two quantities are equal
D. if the relationship cannot be determined from the information given

Solution

Consider ΔOAB

OA = OB = radius

∴ ΔOAB is an isosceles triangle

∴ ∠OAB = ∠OBA = y°

Smallest possible value of x is 20°

∴ Largest possible value of y = ¹⁄₂(180 - 20) = 80°

Largest possible value of x = 50°

∴ Smallest possible value of y = ¹⁄₂(180- 50) = 65°

Range = Maximum Value - Minimum Value

∴ Col. A = 80 - 65 = 15° < Col. B

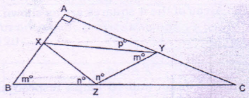
ΔABC is right angles at A. ΔXYZ is inscribed in ΔABC. AB = 3, AC = 4, BC = 5

Measure of angle P in degrees

270° – (2m + 2n)°

A. if the quantity in Column A is greater
B. if the quantity in Column B is greater
C. if the two quantities are equal
D. if the relationship cannot be determined from the information given

Solution

Consider □ABZY

90 + m + 2n + m + p = 360°

∴ 2m + 2n + p = 270°

∴ p = 270°-(2m + 2n)°

∴ Col. A = Col. B

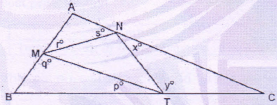
The figure below shows ΔABC and ΔMNT inside it.

p + q + r + s + x + y

270°

A. if the quantity in Column A is greater
B. if the quantity in Column B is greater
C. if the two quantities are equal
D. if the relationship cannot be determined from the information given

Solution

Angles of a triangle add to 180°

Consider ΔMNT

∠m + ∠ + ∠t = 180°

i.e. 180 - (q + r)+ 180 - (s + x)+ 180 - (p + y) = 180°

∴ p + q + r s - s + x + y = 360°

The figure above represents a 16 em piece of string attached to the ends of an 8 em rod. String is now pulled so as to form the Slides of a triangle whose base is the rod.

The greatest possible area of such a triangle in cm²

A. if the quantity in Column A is greater
B. if the quantity in Column B is greater
C. if the two quantities are equal
D. if the relationship cannot be determined from the information given

Solution

A triangle has maximum area when it is an equilateral triangle.

In this case, the side of the equilateral triangle formed measures 8 cm.

∴ Area = ^√3⁄₄ × (8)² = 16√3

Col.A = 16√3 = 16 × 1.732

Col.B = 20 = 16 × 1.25

Attempted

0

Correct

0

Wrong

0

Complete