If f is a fraction between −1 and 1, which of the following must be true?
| A.f7 < f5 |
| B.f6 − f7 < f4 − f5 |
| C.f6 + f7 < f5 + f4 |
| D.(−f)3 < f3 |
| E.f6 < f4 |
-
Solution
B,C and E
Since the problem asks for what must be true, plug in more than once to make sure your final choices are always true. First, let’s say f = 1⁄2. Use your calculator to calculate each answer choice. All five choices are true. Now plug in f = − 1⁄2. This time you eliminate choices (A) and (D).The correct answer is choices (B), (C), and (E).
If p is a negative even integer and q is a positive odd integer, which of the following must be true?
-
Solution
Variables in the answer choices mean Plug In, and the phrase “must be” means you’ll likely have to plug in more than once. Start with p = −2 and q = 3:Eliminate choice (A), because pq = −6; eliminate choice (B), becausep⁄q = 2⁄3 and eliminate choice (C), because p − q = −5.Choices (D) and (E) both work, though, so use new values to test the remaining answers.Try p = −4 and q = 1; now p + q = −3, so eliminate choice (D). Only choice (E), the correct answer, remains.
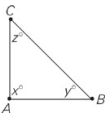
In ΔABC above, x < y + z. What is one possible value of x? [mtextbox][/mtextbox]
-
Solution
0 < x < 90
This problem has a misleading Sgure. Even though x looks like a right angle, it may not be exactly 90 degrees. Use Plugging In to help you. Since all angles of a triangle must add up to 180˚, x + y + z = 180. Since x has to be less than y + z, make y and z add up to be pretty big. For example, you could use y = 50 and z = 60. If you plug in these numbers, then you can calculate x by adding 50 to 60 to get 110.Then subtract from 180. 180 − 110 = 70.This is one possible value of x.
If x < y and 0 < x + y, which of the following must be negative? Indicate all possible values.
| A.−x |
| B.−y |
| C.x − y |
| D.(x − y)2 |
| E.2x − y |
-
Solution
B and C
Use Plugging In to solve this problem. Start by plugging in simple numbers, and keep all the choices that come out negative. If you choose x = 2 and y = 3, then you would keep choice (A), which would equal −2, and choice (B), which would equal −3. Since 2 − 3 = −1, you would keep choice (C). Choice (D) is the same as choice (C), but squared. (−1)2 = 1, so eliminate choice (D). Choice (E) would work out to 2(2) − 3, which equals 1, so eliminate choice (E). Because the problem says “must be,” you will have to Plug In more than once. Try negative this time. If you choose x = −2 and y = 3, x + y = −2 + 3 = 1, so the requirements of the problem are still met. In this case −x is now positive 2, so eliminate choice (A). Choice (B) is still positive, and now you can see that even though x can be negative, y must always be positive to make 0 < x + y, so you can always keep choice (B). Choice (C) calculates to −2 − 3 = −5. You can see that a small number minus a bigger number will always come out to be negative, so keep choice (C).
Points A and B are separated by 50 miles on a straight road. Cyclist A leaves point A, heading toward point B, at a constant speed of 15 miles per hour. At the same time, cyclist B leaves point B, traveling toward point A, at a constant speed of 10 miles per hour. After how many minutes have elapsed will the two meet?
-
Solution
Answer. 120
Cyclists A and B start 50 miles apart and are heading at each other at 15 and 10 miles per hour, respectively.Remember the distance equation is d = r × t.The rates at which the two travel are different, so the distances they will travel will be different; however, since they start at the same time and will meet at the same time (obviously!), their times will be the same.Therefore we can write both of their distance equations:
(1) dA = 15 × t,
(2) dB = 10 × t.
Since their distances together must equal 50 miles, we also know that:
(3) dA + dB = 50.
Now we have three equations with three variables, which means you can use your favorite technique for solving simultaneous equations to find the answer for t. One way is to plug equations (1) and (2) into (3), finding:
15 × t + 10 × t = 50.
Now solve for t, finding t = 2. But wait! You’re not quite done yet. Their speeds were given in miles per hour, and the question asks for the answer in minutes, so you must do a quick conversion: 2 hours × 60 minutes/hour = 120 minutes, which is the correct answer.
If integer a is divisible by both 3 and 14, which of the following must be true?
Indicate all such statements.
-
Solution
A and C
Plug In for a. If a = −42, then it is divisible by 6 and 21 but is not positive or equal to 42, so you can eliminate choices (B) and (D). If a = 84 it is still divisible by 3 and 14, as well as by 21 and 6. In fact, a will always be divisible by 6 and 21, because the prime factors of 3 and 14 are 2, 3, and 7 and the distinct prime factors of 6 and 21 are also 2, 3, and 7. The correct answers are choices (A) and (C).
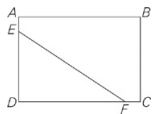
In the rectangle above, AB = x feet,BC = y feet, and AE = FC = 2 feet. What is the area of triangle DEF, in square feet?
-
Solution
Plug in your own numbers for x and y. If x = 4 and y = 5, then the sides of the triangle are 2 and 3.The area of a triangle = 1⁄2bh, so the triangle has an area of 3.Circle 3 as your target. Plugging In shows you that only choice (C) matches your target.
Point A is located on a number line. If point A is between x and y, which are the values on the same number line, and if 0 < x < y,which of the following could represent the position of point A on the number line?
Indicate all possible values.
-
Solution
A, D, and G
Plug in numbers for x and y to solve this problem. Drawing your own number line will also help. If you choose x = 4 and y = 10, then point A will be on the number line between 4 and 10. Choice (A) would be 4 + 1, which equals 5. Since 5 is on the number line between 4 and 10, this could work, so select choice (A). Choice (B) would be 4 − 1, which equals 3. This is not between 4 and 10. Eliminate choice (B). Choice (C) would be 10 + 1. 11 is not on the number line between 4 and 10. Eliminate choice (C). Choice (D) would be 10 − 1. Since 9 is on the number line between 4 and 10, this could work, so select choice (D). Choice (E) would be 4 + 10. 14 is not on the number line between 4 and 10. Eliminate choice (E). Choice (F) would be 4 − 10. −6 is not on the number line between 4 and 10. Eliminate choice (F). Choice (G) would be 10 − 4. 6 is on the number line between 4 and 10, so it could work. Select choice (G).
If 7 orchids cost d dollars, then how many dollars will 10 orchids cost at the same rate?
-
Solution
Plug In. If you choose d = 14, then 7 orchids cost 14 dollars. Since 14 ÷ 7 = 2, one orchid must cost 2 dollars. If one orchid costs 2 dollars, then 10 orchids cost 20 dollars.This makes 20 your target. Use d = 14 for the answer choices.Choice (A) is 70 × 14.This is obviously too big.Choice (B) is 70 ÷ 14, which is also not equal to twenty.Choice (C) is 7 ÷ 10 × 14, which is a fraction, therefore not equal to 20.Choice (D) would be 14 × 10 = 140, which you then divide by 7. Since 140 ÷ 7 = 20, this matches your target. Keep choice (D), but remember to check all five choices on Plugging In problems.Choice (E) would be 14 ÷ 70, which is not equal to 20. Only choice (D) matches your target, so choice (D) is the correct answer.
If for a2⁄3 ≠ 02⁄3 and b ≠ 0, then which of the following statements must be true?
Indicate all possible values.
| A.a⁄b=1 |
| B.a⁄b= -1 |
| C.\(\left ( \frac{a}{b} \right )^{2}=1\) |
| D.a=2⁄3 |
| E.a2 = b2 |
| F.√a = √b |
-
Solution
C and E
For questions that ask about what must be true, you should plan to Plug In more than once. Given the exponents in the question, you want to choose numbers for a and b that are easy to find the cube root for. So, let’s choose a = 8 and b = 8.
(a)2⁄3 = (8)2⁄3 = \(\left ( \sqrt[3]{8} \right )^{2}\) = (2)2 = 4
(b)2⁄3 = (8)2⁄3 = \(\left ( \sqrt[3]{8} \right )^{2}\)
= (2)2 = 4
4 = 4
When you plug 8 into your answer choices, you are able to eliminate choices (B) and (D). Plug In again, but this time change your plugged in value to b = −8 . You should still have a2⁄3 = b2⁄3, but you can now additionally eliminate choices (A) and (F). This leaves choices (C) and (E) as the answers