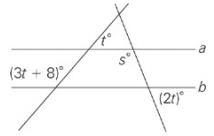
a || b
| Quantity A | Quantity B |
| 95 | s |
-
Solution
First, solve for t: Lines a and b are parallel, so (3t + 8) + t = 180; 4t + 8 = 180; 4t = 172; t = 43. Lines a and b are parallel and you know that 2t + s = 180, so 2(43) + s = 180; 86 + s = 180; s = 94. Quantity A is greater.
What is the area of a regular hexagon with side length 8?
-
Solution
A hexagon has 6 sides.The total number of degrees in the interior of a polygon of n sides is given by (n – 2)180 = (6 – 2)180 = 720. A regular polygon is one in which the sides and angles are all equal. Dividing 720° by 6 gives you 120° for each interior angle in the hexagon. Now draw the hexagon and a point in its center.Connecting the center to each vertex divides the hexagon into six equal triangles.These segments from the center to each vertex are all of equal length, so the triangles are isosceles.These segments also bisect each of the interior angles, so the base angles of these triangles each measure 60°.Thus, the remaining angle in each triangle (near the center of the hexagon) also measures 60°, and therefore these triangles are equilateral, with sides of length 8.The area of an equilateral triangle of side x is \(\frac{x^{2}\sqrt{3}}{4}=\frac{8^{2^{2}}\sqrt{3}}{4}=16\sqrt{3}\) Multiplying the area of each triangle by 6 gives you \(96\sqrt{3}\); the answer is choice (E).
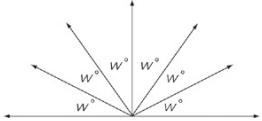
In the figure above, what is the value of w?
-
Solution
There are 180° in a straight line.The straight line is divided into six equal angles in this figure, so 180° ÷ 6 = 30°.
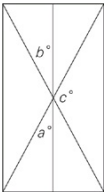
| Quantity A | Quantity B |
| a + b | 180 – c |
-
Solution
Plug in your own numbers, choosing easy values for the angle measures. If a = 40, and b = 60, then the angle in between them must measure 80° to complete the 180° in a straight line.That angle and the angle measuring c° are vertical, so c = 80 as well.Both quantities then equal 100; eliminate choices (A) and (B).Try a new pair of numbers for b and c, and you will realize that plugging in any values yields the same result, making choice (C) the answer.
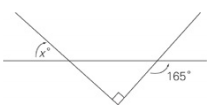
What is the value of x?
-
Solution
Remember that a straight line measures 180°.Therefore, the angle inside the triangle next to the 165° angle measures 180° – 165° = 15°. A triangle contains 180° and a right angle measures 90°.The third angle in that triangle must measure 180° – (90° + 15°) = 75°. Vertical angles are equal, so x = 75.The answer is choice (D).
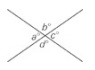
In the figure above, c is 4⁄5 of d. What is the value of c ?
-
Solution
The sum of c and d is 180, so you know that 4⁄5d + d = 180. Solve this equation: d = 100. If d = 100, then c = 80.The answer is choice (B).

If X is the center of the circle above, then what is the sum of the measures of ∠WXY and ∠VXZ?
-
Solution
Because ∠WXY forms a line with a 60° angle, it must be 180° – 60° = 120°; ∠WXY and ∠VXZ are vertical angles, so ∠VXZ must be 120° as well.The sum of the measures of ∠WXY and ∠VXZ is 120° + 120° = 240°.
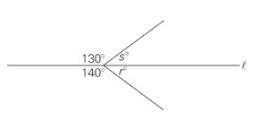
| Quantity A | Quantity B |
| r | s |
-
Solution
Use the Rule of 180 to find r = 40 and s = 50
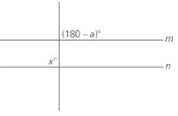
m\(\mid \mid\)n
| Quantity A | Quantity B |
| a | 90 |
-
Solution
Two parallel lines—with a line cutting through them—create big angles (bigger than 90°) and small angles (smaller than 90°). Any big angle plus any small angle equals 180°. In the figure, x appears to be a big angle and (180 – a) appears to be a small angle. So x + (180° – a) = 180°, or x = a.But in fact, because you can’t trust the figure, you don’t know whether x (and therefore a) is really a big, small, or 90° angle.The answer is choice (D).
For which of the following values of x is an integer?
Indicate \(\underline{all}\) possible values.
-
Solution
A,C, and G
This algebra question has numbers for answer choices, so set up your scratch paper to Plug In the Answers and look for an integer answer. If x = 2, then \(\frac{4^{2}}{2^{4}}=\frac{16}{16}=1\), so choice (A) works. If x = 3, then \(\frac{4^{2}}{2^{4}}=\frac{16}{16}=1\), so eliminate choice (B). If x = 4, then \(\frac{4^{2}}{2^{4}}=\frac{16}{16}=1\), so choice (C) works. If x = 5, then \(\frac{4^{2}}{2^{4}}=\frac{16}{16}=1\) isn’t an integer, since you cannot cancel all the 5’s in the denominator; eliminate choice (D).You could calculate it, but it’s easier to think in terms of reducing the fraction. Likewise in choice (E),\(\frac{4^{6}}{6^{4}}\) isn’t an integer, because each of the 6’s in the denominator has a 2 you can cancel, but a 3 you cannot cancel.Eliminate choice (E) as well as (F), since it too is not an integer. Finally, is an integer:Expand it out to \(\frac{4\times4\times4\times4\times4\times4\times4\times4}{8\times 8\times 8\times 8}=\frac{4\times4\times4\times4\times4\times4\times4\times4}{4\times 2\times 4\times 2\times 4\times 2\times 4\times 2}\) which cancels down to all 1’s and 2’s.Choices (A), (C), and (G) are correct.