Towns A,B, and C lie in a plane but do not lie on a straight line. The distance between Towns A and B is 40 miles, and the distance between Towns A and C is 110 miles.
| Quantity A | Quantity B |
| The distance between Towns B and C | 60 miles |
-
Solution
If the towns do not lie on a straight line, they must lie on a triangle; Quantity A represents the third side of the triangle. According to the Third Side Rule this side must be greater than the difference between, and less than the sum of, of the other two sides.Thus, Quantity A lies between 110 − 40 = 70 miles and 110 + 40 = 150 miles, but is always greater than 60 miles; the answer is choice (A).
| Quantity A | Quantity B |
| The area of an equilateral triangle with a side length of 4 | The area of an isosceles right triangle with a hypotenuse of 4√2 |
-
Solution
In Quantity A, an equilateral triangle with a side length of 4 has a base of 4 and a height of 2√3: remember, an equilateral triangle cut in half yields two 30-60-90 triangles.Thus, the triangle has an area of 1⁄2 × 4 × 2√3, or .Remember that √3 is approximately 1.7, so 4√3 is about 6.8. In Quantity B, “isosceles right triangle” means 45-45-90, so a long side of 4√2 yields a base and a height both equal to 4, and an area of 1⁄2 × 4 × 4, or 8. Quantity B is greater.
Mei is building a garden in the shape of an isosceles triangle with one side of 10. If the perimeter of the garden is 32, which of the following is a possible area of the garden?
-
Solution
If the triangle is isosceles, it must have two equal sides; thus, the triangle could have sides of 10, 10, and 12 or sides of 10, 11, and 11. To find one of the possible areas, draw out your 10-10-12 triangle. With the height drawn in, it should look like this:

Note that the big triangle divides nicely into two of the familiar 6-8-10 triangles; you now have a triangle with a base of 12 and a height of 8, so the area is 1⁄2 × 12 × 8 = 48.The answer is choice (B).
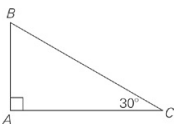
If the area of the above triangle is 8√3, what is the length of side AB?
-
Solution
Plug in the answers, and be sure to note that this is a 30-60-90 triangle. In choice (B), if AB is 4 and AC is 4√3, then the area is 1⁄2(4)(4√3)=8√3. So the answer is choice (B).
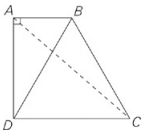
| Quantity A | Quantity B |
| (AB)2 + (AD)2 | (AC)2 |
-
Solution
Although the Pythagorean theorem dictates that (AB)2 + (AD)2—the sum of the squares of two sides of a right triangle—is equal to the square of the hypotenuse, or (BD)2, there’s no way to determine the relationship between (BD)2 and (AC)2.Remember, figures are not drawn to scale on the GRE: Although it looks like AC is longer than BD, it’s possible to redraw the figure so that either segment is longer; try varying the length of DC.
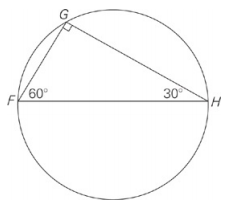
In the figure above, FG = 4, and FH is a diameter of the circle. What is the area of the circle?
-
Solution
This is a 30-60-90 triangle, so FH = 8. If the diameter is 8, then the radius is 4, so the area is 16π.
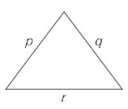
| Quantity A | Quantity B |
| r | p + q − 1 |
-
Solution
According to the Third Side Rule, r must be less than the sum of p and q. Plug In to test if r is less than p + q − 1. Let p = 5 and q = 4. If r = 2, Quantity A is 2 and Quantity B is 8; Quantity B is greater, so eliminate choices (A) and (C). However, a value of 8 for r would also satisfy the Third Side Rule; now the quantities are equal, so eliminate choice (B) and select choice (D).
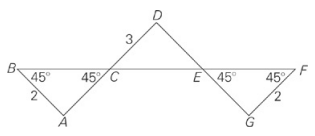
| Quantity A | Quantity B |
| BF | 7√2 |
-
Solution
Although the figure may look complex, it’s really just three 45-45-90 triangles attached end-to-end;BF is the sum of the long sides of the three triangles. If AB = 2, then AC = 2, and BC = 2√2; similarly,EG and FG are 2, and EF = 2√2.Two of the angles in triangle DCE are vertical angles with 45° angles in the other two triangles, so it must be a 45-45-90 triangle also—the legs are each 3, so CE = 3√2. So BF = 2√2 + 2√2 + 3√2 =7√2; the quantities are equal.
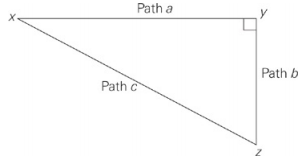
John and James walk from point x to point z (shown in the figure above). John walks directly from x to y on Path a and then directly from y to z on Path b. James walks directly from x to z on Path c. If Path a is 13 miles long and Path b is 5 miles long, John walks about how many miles longer than James?
-
Solution
Use the Pythagorean theorem to find the length of path C: 52 + 132 = c2. So path c is approximately 14 miles. John walks 18 miles, and James walks 14 miles, so the answer is choice (C).
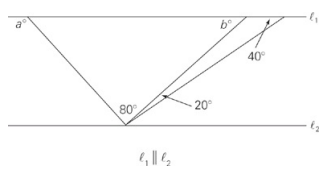
| Quantity A | Quantity B |
| a + b | 200 |
-
Solution
Start by finding the remaining angles of the triangle on the right: If the two small angles add up to 20° + 40° = 60°, then the unmarked angle must be 120°, and b must be 60.The remaining angle in the triangle on the left must be 40°, and a must be 140. So Quantity A is 140 + 60 = 200; the quantities are equal.
