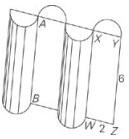
Rectangle WXYZ has a length of 6 and a width of 2. Rectangle AYZB bisects right cylinders ABC and D. If all the cylinders have the same radius, what is the combined volume of the four half-cylinders?
-
Solution
The four half-cylinders are equivalent to two cylinders of radius 1, whose total volume will therefore be 2(π126) = 12π.The answer is choice (C).
A circle is inscribed in a square with area 36. What is the area of the circle?
-
Solution
9π
First, draw the circle inside a square.Because the square has an area of 36, each side is 6.This means that the diameter of the circle is 6 and the radius is 3. Using the circle area formula, the answer is 9π.
A circle with a circumference of 12π is divided into three sectors with areas in a ratio of 3:4:5. What is the area of the largest sector?
-
Solution
The diameter of the circle is 12, so the radius is 6, and the area is 36π.The total number of parts in the ratio is 3 + 4 + 5 = 12, so each part covers an area of \(\frac{36\pi }{12}\) = 3π.The largest ratio part is 5 times this amount, or 15π.
A square has edges of length 12 inches.
| Quantity A | Quantity B |
| 24π | The area of the largest circle that can fit inside the square |
-
Solution
For Quantity B, the side of the square is the same length as the diameter of the circle.The diameter is twice the radius, so the radius is 6. Plug this into the formula for area: A = πr2 to find that A = 36π. Quantity B is greater.
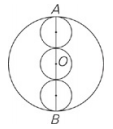
Line AB passes through the center of circle O and through the centers of each of the 3 identical smaller circles. Each circle touches two other circles at exactly one point each.
| Quantity A | Quantity B |
| The circumference of circle O | The sum of the circumferences of the 3 smaller circles |
-
Solution
Start by plugging in a radius for the smaller circles; try r = 2.The circumference of each circle is 2πr = 4π, and the sum of all three circumferences is 12π.Because the diameter of circle O is equal to the sum of the 3 shorter diameters, the diameter of circle O is 4 + 4 + 4 = 12, its radius is 6, and its circumference is 12π, so the quantities are equal.
| Quantity A | Quantity B |
| The area of a square with a perimeter of p | The area of a circle with a circumference of p |
-
Solution
Plug in a value for p. If p = 8, then the side of the square is 2 and the area is 4. If the circumference of the circle is 8, then the radius is 4⁄π, and the area is \(\frac{16}{\pi }\)—approximately 5. Quantity B is larger. Plug in another value for p and you will find that Quantity B remains larger.
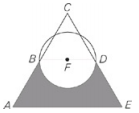
Triangle ACE is equilateral with side lengths of 8. Points B and D are the midpoints of line segments AC and CE respectively. Line segment BD is a diameter of the circle with center F. What is the area of the shaded region?
-
Solution
To find the shaded region, subtract the unshaded region (the triangle and semicircle) from the entire triangle.The area of an equilateral triangle of side x is \(\frac{x^{2}\sqrt{3}}{4}=\frac{8^{2}\sqrt{3}}{4}=16\sqrt{3}\).Triangle BCD is also equilateral, and has sides of length 4, so its area is \(\frac{x^{2}\sqrt{3}}{4}=4\sqrt{3}\).The radius of the circle is 2, so the area of the semicircle is \(\left ( \frac{1}{2} \right )\pi r^{2}=\left (\frac{1}{2} \right )\pi 2^{2}=2\pi\). So the answer is 16√3 - 4√3 - 2π = 12√3 - 2π.
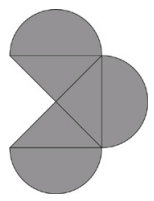
The diameters of the semicircles above are 8, and the diameter of the semicircle on the right is perpendicular to those of the other two semicircles. What is the total area of the shaded region?
-
Solution
Draw a fourth triangle and semicircle, and you can see that the figure shown represents 11⁄2 circles and 3⁄4 of a square.Because the three diameters are perpendicular and congruent, they represent three sides of a square; the isosceles right triangles shown constitute three of the four triangles in the completed square.The area of a circle with diameter of 8 (and radius of 4) is πr2 = 16π.11⁄2 times this area is 24π.Eliminate choices (A), (D), and (E) because they do not contain 24π.The diameter of each semicircle is the length of the side of the square.The area of the entire square would be s2 = 82 = 64.
3⁄4 of this area is 48. Adding the two areas together gives you the expression in choice (C).
The height of a right circular cylinder is increased by p percent and the radius is decreased by p percent.
| Quantity A | Quantity B |
| The volume of the cylinder if p = 10 | The volume of the cylinder if p = 20 |
-
Solution
Plug in 10 for the height and radius of the cylinder. So Quantity A is πr2h = π9211 = 891π. Quantity B is π8212 = 768π
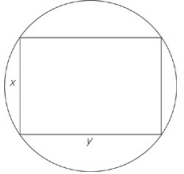
In the figure above, a rectangle is inscribed in a circle. Lengths x and y are both integers such that x + y = 10, and 1 < x < y. Which of the following are possible values for the diameter of the circle?
Indicate \(\underline{all}\) possible values.
-
Solution
C, D, and F
Consider all the possible different integer pairs for the dimensions of the rectangle.You cannot try the integer pair of 1 and 9 or 5 and 5, because you know that x < y. If the rectangle has sides of 4 and 6, you can solve for the diagonal (equal to the circle’s diameter) with the Pythagorean theorem, which gives you [latex]\sqrt{52}[/latex] or 2[latex]\sqrt{13}[/latex], correct choice (C). If the rectangle has sides of 3 and 7, the diagonal is \(\sqrt{58}\), correct choice (D). If the rectangle has sides of 2 and 8, the diagonal is \(\sqrt{58}\), or 2\(\sqrt{58}\), correct choice (F).