In the rectangular coordinate system above, if the area of right triangle DEF is 15, then which of the following are the coordinates of point D ?

(−4, −1)
(−2, −1)
(−2, 4)
(1, −1)
It cannot be determined from the information given.

Solution

Subtracting the y-coordinates of the given points gives you the length of leg EF: 4 − (–1) = 5.The area formula for a triangle will give you the length of the other leg, DF:¹⁄₂ bh=¹⁄₂ (b)(5);b=6, which equals 15. Subtracting 6 from the x-coordinate of F gives you the x-coordinate of D, and D has the same y-coordinate as F. So the coordinates of D are (–2, –1); the answer is choice (B).

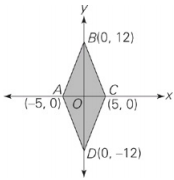
Quantity A	Quantity B
The perimeter of quadrilateral ABCD	The area of the shaded region

Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
The relationship cannot be determined from the information given.

Solution

The axes split the quadrilateral into four equal 5-12-13 right triangles (note the highly suspicious numbers on the drawing). So the perimeter is 4(13) = 52, and Quantity B is therefore greater.

On the number line shown above, the coordinates of points P and Q are –⁴⁄₂ and 2, respectively.

Quantity A	Quantity B
¹⁄₂	The coordinate of the midpoint of line segmentPQ

Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
The relationship cannot be determined from the information given.

Solution

The distance between P and Q is 6(²⁄₃) ticks, so the midpoint will be 3(¹⁄₂) ticks from either endpoint, which is the first tick to the right of 0, at ¹⁄₃.To find the coordinate of the midpoint, simply average the coordinates of the endpoints: . so Quantity A is greater. Alternatively, because the smaller ticks divide each unit into 3 equal parts, they represent lengths of ¹⁄₃.

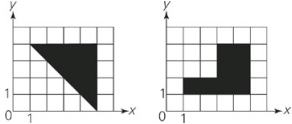
Quantity A	Quantity B
The area of the shaded region in Figure A	The area of the shaded region in Figure B

Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
The relationship cannot be determined from the information given.

Solution

Figure A contains 6 whole boxes plus 4 half-boxes, for a total of 8. Figure B contains 8 whole boxes.The answer is choice (C). Alternatively, the area of the right triangle in Figure A is ¹⁄₂bh= ¹⁄₂(4)(4)=8 and Figure B contains a rectangle plus two units whose total area is bh=(3)(2)=6;6+2=8.

Paul and Allen are choosing ties out of a selection of three distinct red ties,five distinct green ties, and six distinct blue ties. If Paul and Allen each wear one tie, how many different ways could they wear ties of the same color?

Solution

56

This problem involves permutations, because the order matters since the ties are all distinct. Start with Paul wearing a red tie. He has 3 red tie choices and Allen has 2 remaining red tie choices, giving them a product of 6 permutations. For green ties, they have 5 × 4 = 20 permutations. For blue ties, they have 6 × 5 = 30 permutations.The grand total is 56 permutations

For his birthday,Brian will receive either three or four differently colored ties, either two or three differently colored shirts, and either one or two differently colored jackets. Depending on how many ties, shirts, and jackets he receives, which of the following values could be the number of ways he could make an outfit with one tie, one shirt, and one jacket?

Indicate all possible values.

Solution

A,B,C,E, F,and G

Rather than writing out every possible outcome, see if you can express the answer choices as the product of 3 factors that could be the number of ties, shirts, and jackets Brian receives.Choice (A) is possible: 3 ties × 2 shirts × 1 jacket = 6 outfits.Choice (B) is possible: 4 ties × 2 shirts × 1 jacket = 8 outfits.Choice (C) is possible: 3 ties × 3 shirts × 1 jacket = 9 outfits.Choice (D) is not possible: you’d need a 5 as a factor to get to 10, and Brian can’t receive 5 of anything, so eliminate choice (D).Choice (E) is possible in 2 different ways: 3 ties × 2 shirts × 2 jackets = 12 outfits, as does 4 ties × 3 shirts × 1 jacket.Choice (F) is possible: 4 ties × 2 shirts × 2 jackets = 16 outfits. And, finally, choice (G) is possible: 3 ties × 3 shirts × 2 jackets = 18 outfits. All of the choices except choice (D) work.

All employees at Company W are assigned unique employee ID codes that consist of numbers and letters from the alphabet. If letters can be repeated within the same code but numbers cannot, which of the following must be true?

There are 2,600 possible different 3 digit codes consisting of 1 letter and 2 digits.
There are 60,840 possible different 4 digit codes consisting of 2 letters and 2 numbers.
There are 650 possible 2 digit codes consisting of 1 letter and 1 digit.

Solution

B

This is a permutation problem, so lay out your slots to fill and then multiply. For choice (A) you have 1 slot for a letter and two slots for digits.There are 26 choices for your letter and 10 choices for your first digit.Because you can’t repeat digits, there are 9 choices for your second digit.Thus, the number of different codes that can be made is 26 × 10 × 9 = 2,340.Eliminate choice (A). For correct choice (B), you have two spots for letters and two for digits, so you have 26 × 26 (letters can repeat) × 10 × 9 = 60,840. Choice (C) is incorrect because the number of different codes consisting of one letter and one digit is 26 × 10 = 260.The only correct answer is choice (B).

Sherry supervises a crew of maintenance engineers for an office building. If there are 5 experienced maintenance engineers and 3 apprentice engineers and the engineers are sent out on jobs in teams, which of the following must be true?

Indicate all possible values.

A.There are 10 different 3-person teams of experienced engineers she could send.
B.There are 3 different 2-person teams of apprentice engineers she could send.
C.There are 2 different 2-person teams of apprentice engineers she could send.
D.There are 10 different 2-person teams of experienced engineers she could send.
E.There are 10 different 4-person teams of experienced engineers she could send.

Solution

A,B, and D

Starting with choice (A), there are 3 slots on the team, with 5 experienced engineers available for the first slot, 4 for the second slot, and 3 for the third slot. Order doesn’t matter, so divide by 3! to get \(\frac{5\times 4\times 3}{3\times 2\times 1}\) = 10.Choice (A) is correct. For choice (B), you have 3 apprentice engineers available for 2 slots and once again, order doesn’t matter.\(\frac{3\times 2}{1\times 2}\) = 3.Choice (B) is correct and you can eliminate choice (C), which contradicts choice (B). For choice (D) you have = 10, so choice (D) is correct.Choice (E) is incorrect because \(\frac{5\times 4}{1\times 2}\) = 5.The correct answers are choices (A), (B), and (D).

Twelve runners enter a race to compete for first, second, and third place. How many different combinations of winners are possible?

Solution

1,320

In this case, order matters, so you simply need to multiply the number of possible runners for each spot.That should look like this: 12 11 10 = 1,320.

Mark can take three friends with him on a vacation and is listing the possible combinations of friends. If he has five friends to choose from and is numbering each possible combination sequentially beginning with 1, which of the following numbers will appear on his list of combinations?

Indicate all possible values.

Solution

A,B

The order of friends doesn’t matter.There are five friends to choose from for three spots, so the top of your fraction should read: 5 4 3, and to correct for the order of friends not mattering, the bottom of your fraction should be: 3 2 1.\(\frac{5\times 4\times 3}{3\times 2\times 1}\) = 10. Since he is numbering possibilities sequentially, the numbers 1 through 10 will be on the list, making choices (A) and (B) correct

Attempted

0

Correct

0

Wrong

0

Complete