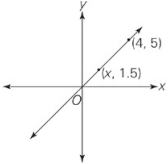
What is the value of x in the rectangular coordinate system above?
-
Solution
Note that the line contains three points: (0, 0), (4, 5), and (x, 1.5).The slope between any two of these points is the same.Remember that slope is change in y over change in x.Thus,\(\frac{5-0}{4-0}=\frac{1.5-0}{x-0}\), or \(\frac{5-0}{4-0}=\frac{1.5-0}{x-0}\).Cross-multiply to find 5x = 6.0. Divide by 5 to find x = 1.2.The answer is choice (B).
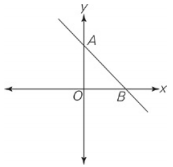
The equation of the line graphed on the rectangular coordinate system above is given by:
\(y=-\frac{13}{12}x+8\)| Quantity A | Quantity B |
| AO | BO |
-
Solution
Although you have enough information to find the exact values of AO and BO, it’s not necessary to do so to compare the quantities. The slope of the line is \(-\frac{13}{12}\), which means that the vertical distance, or rise, is greater than the horizontal distance, or run, by a ratio of 13 to 12 (you’re dealing with distances on a coordinate plane, so disregard the negative sign).Because AO and BO are equal to, respectively, the rise and the run of the same segment of the line, Quantity A is greater.

Point X is at (a, b).
| Quantity A | Quantity B |
| −a | b |
-
Solution
Point X is at approximately (2, –1.5). So Quantity A is about –2 and Quantity B is about –1.5, thus, Quantity B is greater
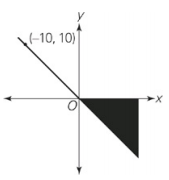
Which of the following pairs of coordinates corresponds to a point in the shaded region of the graph shown above?
-
Solution
Use Process of Elimination to solve this one. First, only coordinate pairs with a positive x-value and a negative y-value will fall in the proper quadrant, so eliminate choices (B), (C), and (E).The line that divides the correct quadrant into shaded and unshaded regions has a slope of –1 because it goes through the origin and the point (–10, 10). On this line, the absolute value of the x-coordinate equals the absolute value of the y-coordinate. In the shaded region, then, |x| > |y|, so choice (D) can be eliminated. Only choice (A) remains. Alternatively, realize that this figure is drawn accurately, because of the placement of (10, –10), and plot all 5 points, eliminating all of those that fall outside the shaded region.

Points (a, b) and (c, d), not shown in the figure above, are in quadrants I and III, respectively. If abcd ≠ 0, then the point (−bd, bc) must be in which quadrant?
-
Solution
Plug in points in the appropriate quadrants. If (a, b) = (1, 2) and (c, d) = (–3, –4), then the point in question is (−bd, bc) = [−(2)(–4), (2)(–3)] = (8, –6), which is in quadrant IV; the answer is choice (D).
Which of the following is the graph of the equation y = −|−x| ?
-
Solution
Plug values into the equation and eliminate graphs that do not include those values. If x = 1, then y = –1; eliminate choices (B) and (D). If x = –1, then y = –1, eliminate choices (A) and (E). Only choice (C) remains.
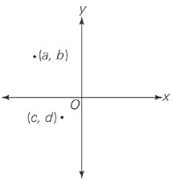
| Quantity A | Quantity B |
| bd | ac |
-
Solution
Point (a, b) is in the second quadrant where points have signs of (–, +); thus, a is negative and b is positive. Point (c, d) is in the third quadrant where points have signs of (–, –); thus, c is negative and d is negative. So, Quantity A is a positive times a negative, which is negative. Quantity B is a negative times a negative, which is positive. Quantity B must be greater.
Cam’s home is 2 miles east and 3 miles north of Atlanta. He drives to town B, which is 3 miles east and 9 miles north of his home.
| Quantity A | Quantity B |
| The shortest distance between town B and Atlanta | 17 miles |
-
Solution
Draw a rectangular coordinate system with Atlanta as the origin, i.e., the point (0, 0). So Cam’s home is at (2, 3). Going 3 miles east and 9 miles north puts town B at (5, 12). Quantity A is the straight line distance from (0, 0) to (5, 12).Connecting these two points creates the hypotenuse of a 5-12-13 right triangle, so Quantity A is 13, and the answer is choice (B).

Line segment BC is parallel to the x-axis.
Line segment AC is parallel to the y-axis.
| Quantity A | Quantity B |
| d | e |
-
Solution
Point C has the same x-coordinate as point A and the same y-coordinate as point B.The coordinates of C are therefore (1, 1), so the quantities are equal.
On the coordinate axes shown above, the graph of y = 4x + 20 would cross the x-axis at the point where
-
Solution
On the x-axis, y = 0; eliminate choices (B), (C), and (D).Then plug in 0 for y in the given equation. Solve for x: 0 = 4x + 20, so x = –5, and the answer is choice (A).