In a recent election, James received 0.5% of 2000 votes cast. To win the election, a candidate must receive more than 50% of votes. How many minimum additional votes would James have needed to win the election?

A. 901
B. 989
C. 990
D. 991
E. 1001

Solution

James received 0.5% of 2000 votes, i.e. 10 votes.

To win the election, he must have (0.5 × 2000) + 1 = 1001 votes.

∴ He must have minimum 1001 - 10 = 991 additional votes.

For how many integers n is 2ⁿ = n²?

A. None
B. 1
C. More than 3
D. 2
E. 3

Solution

For n = 2, 2ⁿ = n² = 4

For n = 4, 2⁴ = 4² = 16

For n > 4, 2ⁿ > n?

∴ Only for 2 values of n, namely 2 and 4, 2ⁿ = n²

In the circle above, PQ is parallel to the diameter OR, OR has length 18 units. What is the length of minor arc PQ?

A. 2π
B. $\frac{9\pi }{4}$
C. $\frac{7\pi }{2}$
D. $\frac{9\pi }{2}$
E. 3π

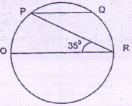
Solution

Let origin be 'A'.

Join PA. ∴ ΔAPR is isosceles triangle.

∴ ∠PAR 110°

∴ ∠PAO is 70°

∴ Measure of arc PO is 70°. Similarly measure of arc QR is 70°.

∴ arc PQ is 180° - 70° - 70° = 40°

∴ arc PQ = $\frac{40}{360}$ × 18°= 2°

In rectangular co-ordinate system shown below line y = x is perpendicular bisector of segment AB (not shown) and x-axis is perpendicular bisector of segment Be (not shown). If co-ordinates of point A are (2, 3), what are the co-ordinates of point C?

A. -3,-2
B. -3,2
C. 2,-3
D. 3,-2
E. 2, 3

Solution

Line y = x has slope 1 i.e. any point on this line has same value for x and y coordinates. Also this line is a perpendicular bisector of AS. So B is a reflection of A through this line. So coordinates of A get interchanged to get the coordinates of B.

∴ B is (3, 2)

Similarly X-axis is perpendicular bisector of BC, C is reflection of B through X-axis.

∴ x co-ordinates of C and B are same, and y co-ordinates of C and B are same and y co-ordinate of C is negative of y co-ordinates of B.

∴ C has co-ordinates (3, -2)

Note: Co-ordinates of Band C can also obtained by the mid-point formula

For any integer n greater than 1, n! denotes the product of all integers from 1 to n, inclusive. How many prime numbers are there between 6! + 2 and 6! + 6 inclusive?

A. 0
B. 1
C. 2
D. 3
E. 4

Solution

61 = 720

∴ 61 + 2 = 722

61 + 6 = 726

722,724,726 are divisible by 2.

725 is divisible by 5.

723 is divisible by 3 as the sum of the digits is divisible by 3.

∴ None of the 5 numbers are prime numbers.

A store currently charges same price for each towel that it sells. If current price of each towel was to be increased by $1, 10 numbers of fewer towels could be bought for $120, excluding sales tax. What is the current price of each towel?

A. $1
B. $2
C. $3
D. $4
E. $12

Solution

First method: Try options

Second method: Let price per Towel be 'P'

∴ equation will be

$\frac{120}{P}=\frac{120}{P+l}+10$

∴ 0 = $\frac{120P -120P -120}{P(P+1)}+10$

0= -120 + 10p² + 10P

0 = P2+P-12

0 = (P + 4)(P - 3)

Since P cannot be -4, it has to be 3.

The ratio, by volume of soap to alcohol to water in certain solution is 2 : 50 : 100. The solution will be altered so that ratio of soap to alcohol is doubled while ratio of soap to water is halved. If altered solution will contain 100 cubic centimeters of alcohol, how many cubic centimeter of water will it contain?

A. 50
B. 200
C. 400
D. 625
E. 800

Solution

The original ratio is 2:50:100.

When the ratio 2 : 50 is doubled, new ratio is 4:50.

Similarly when ratio 2:100 is halved new ratio will be 1:100 which is the same as 4:400.

∴ The new ratio = 4:50:400

Since 100 cu. cm. represents 50 parts of alcohol in new solution, 800 cu. cm. will represent 400 parts of water in solution.

If ‘a’ is a positive integer, and if unit’s digit of a² is 9 and the unit’s digit of (a + 1)² is 4, what is unit’s digit of (a+2)²?

A. 1
B. 3
C. 5
D. 7
E. 9

Solution

a is an integer and unit's digit of a² is 9.

∴ a can be 3 (3² = 9) or 7 (7² = 49)

But 3 does not satisfy the second condition i.e. (a+1)²= (3+1)²= 16.

We need unit's digit as 4.

∴ 7 is the correct answer.

(7+1)²= 64 i.e. unit's digit is 4.

∴ (7 + 2)² = 81 unit's digit is l.

In XY co-ordinate system if (a, b) and (a + 3, b + k) are two points on line defined by the equation x = 3y -7, then k =

A. 1
B. 3
C. 5
D. 7
E. 9

Solution

Since the two points lie on the line, they satisfy the equation of the line. So the slope is the same.

Consider x = 3y - 7

∴ $y=\frac{x}{3}+\frac{7}{3}$ ∴ Slope = ¹⁄₃

∴ $\frac{b + k - b}{a+3-a}=\frac{1}{3}$ ∴ ^k⁄₃ = ¹⁄₃ ∴ k = 1

What is the units digit of (13)⁴x (17)²X (29)³

A. 9
B. 7
C. 5
D. 3
E. 1

Solution

The units digit of (13)⁴ = 1, since 34 = 81

The units digit of (17)² = 9

The units digit of (29)³ = 9, since 9³ = 72$\underline{9}$.

∴ The units digit of (13)⁴ × (17)² × (29)³ = 1

as 1 × 9 × 9 = 8$\underline{1}$

Attempted

0

Correct

0

Wrong

0

Complete