Month Average price per dozen
April $1.26
May $ 1.20
June $ 1.08

The table above shows average price per dozen of large grade A eggs sold in a certain store during three successive months. If 2/3 as many dozen eggs were sold in April as in May and twice as many were sold in June as in April, what was the average price per dozen of eggs sold over three months period?

A. $ 1.08
B. $ 1.10
C. $ 1.14
D. $ 1.16
E. $ 1.18

Solution

Let Eggs sold in the month of May are 3 dozen.

∴ Eggs sold in the month of April will be 2 dozen and June will be 4 dozen.

Average will be

$\frac{(1.12\times 2)+ (1.20\times 3)+ (1.08\times 4)}{9}=1.16$

If n is an integer and n =$\frac{2 \times 3 \times 5 \times 7 \times 11\times 13}{77k}$ then which of the following could be the value of k?

A. 22
B. 26
C. 35
D. 54
E. 60

Solution

n=$\frac{2\times 3\times 5\times 7\times 11\times 13 }{7\times 11\times k}=\frac{2\times 3\times 5\times 13}{k}=\frac{390}{k}$

For n to be an integer, k has to be a factor of 390.

i.e. 13 × 2 = 26

There is a square plot measuring x feet on each side. Plot consists of rectangular garden, 48 square feet in area, surrounded by a walk that is 3 ft. wide on two opposite sides and 2 ft. wide on other two opposite sides. What is the measurement of side of the square?

A. 8
B. 10
C. 12
D. 16
E. 18

Solution

The dimensions of rectangle are (x - 6) and (x- 40)

∴ (x - 6)(x - 4) = 48

X² - 10x - 24 = 0 ∴ (x - 12) (x + 2) = 0

∴ x = 12

200 gm of a solution was 10% sugar by weight. 50 gm were replaced by a second solution; resulting in a solution that was 16% sugar by weight. The second solution was what percent sugar by weight?

A. 34%
B. 24%
C. 22%
D. 18%
E. 8.5%

Solution

The total solution after replacement is 16%, Hence total sugar now is 32 gm, Thus 17 gm of sugar was added by the second solution of 50 gm, Hence 2nd Solution contains 34% sugar.

If 0 < n < 1, which of the following must be greater than 1?

A. $\frac{3n}{2}$
B. $\frac{3n}{2}$
C. $\frac{n}{n^{2} + 1}$
D. $\frac{1}{1+n}$
E. $\frac{3}{2+n}$

Solution

n is a positive fraction less than 1.

(A) $\frac{3n}{2}$ > 1 only if n > ²⁄₃., which may not be necessary.

(B) $\frac{n}{1-n}$ > 1 only if n > 1 - n or 2n > 1 or n > 1/2 , which is not necessary for 'n'

(C) $\frac{n}{n^{2}+1}$ can never be> 1, because 'n' is always less than 1.

So, 1 + n2 will be always greater than 'n'.

(D) $\frac{1}{1+n}$ will be always less than 1 for the reason, 'n' is always greater than zero.

(E) $\frac{3}{2+n}$ will be always greater than 1 as, n is always less than 1 but more than zero.

∴ (2+ n) always < 3.

50% of subscribers to newspaper x are corporate managers and of these 30% are in financial field. If 40% of subscribers who are corporate managers in financial world are money managers, how many of newspaper’s 25,000 subscribers are corporate money managers in financial field?

A. 1500
B. 3000
C. 3750
D. 7500
E. 8750

Solution

30% of 50% of 25,000 subscribers are in financial field. 3750 subscribers are corporate managers in financial field. Further 40% of 3750 are money managers in financial field.

∴ Required number is 40% of 3750 = 1500.

n, 2n – 1, 2n +1 are sides of a right angled triangle. What is the value of n?

A. 1.5
B. 2√2
C. 8
D. 5
E. 10

Solution

By Pythagoras theorem (2n + 1)² = (n)² + (2n - 1)²

∴ 4n² + 4n + 1 = n² + 4n² + 1 - 4n

∴ n² = 8n ∴ n = 0, n = 8

N ≠ 0 as dimension cannot be zero

A and B are independent events. Probability of occurrence of A is 0.6 and that of B is 0.8. Find the probability of occurrence of A or B or both.

A. 1.0
B. 0.9
C. 0.92
D. 0.95
E. 0.82

Solution

P(A ∪ B) = P(B) - P(A(∩)B)

Since A and B are independent events,

P(A(∩)B) = P(A)× P(B)

∴ P(A ∪ B) = 0.6 + 0,8 - 0.6 x 0.8

= 0.92

The figure above shows a bicycle path. If semicircular portion ABC is 100 π and CD is 100 ft. then what is AD?

A. 200√3
B. 200
C. 50√3
D. 100
E. 100√3

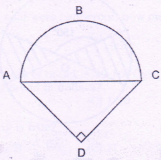
Solution

AC is the diameter as it subtends a. semicircular arc ABC

∴ $\frac{\pi (AC)}{2}$= 100π ∴ AC = 200 m.

By Pythagoras theorem (AC)² = (AD)² + (CD)²

200² = AD² + 100²

∴ AD = $\sqrt{30000}$ ∴ AD = 100√3

The table above shows results of a survey of 200 people who were asked if they were members of any of the following groups.

(I) Regular Churchgoers

(II) Registered Voters

(III) High-school graduates.

How many of those responding to survey were high-school graduates?

A. 13
B. 33
C. 48
D. 81
E. 106

Solution

This category includes the categories III only, I & III only, II & III only, I, II, III only.

∴ Required number = 13 + 20 + 25 + 48 = 106

Attempted

0

Correct

0

Wrong

0

Complete