On a certain 16 question test, each question is worth 4 points more than the previous question. If the greatest number of points that can be scored on the test is 528, how many points is 11th question worth?
-
Solution
It is an arithmetic progression with first term a, common difference d = 4, and sum of the 16 terms = 528.
Sn = n⁄2[2a + (n - 1)d]
∴ 528 = \(\frac{16}{2}\)[2a + (16 - 1) × 4] ∴a = 3
11th question worth = 11th term in the A.P.
∴ t11 = a + 10d = 3 + (10 × 4) = 43
Paul works as a research scientist in a defense organization. In performing a sequence of experiments, he made 25 measurements. The average of these measurements was 19. For security reasons, scientist coded the data by multiplying each of the measurements by 12 and then adding 27 to each product. What is the average of coded measurements?
-
Solution
The average of 25 measurements is 19.
Since each measurement is multiplied by 12, the average also gets multiplied by 12.
Similarly, the average increases by 27 after multiplication.
∴ New Average = (19 × 12)+ 27 = 255
If goods be purchased for $450 and one third be sold at a loss of 10%, at what gain % should the remainder be sold so as to gain 20% on the whole transaction?
-
Solution
Cost of 1⁄3 of goods = $150
Selling Price of 1⁄3 of goods = 150 × \(\frac{90}{100}\) = $135
Total selling price is to be $450 × \(\frac{120}{100}\) = $540
∴ S.P. of remaining 2⁄3 of goods
= 540 - 135 = 405
∴ Profit % = \(\frac{105}{300}\) × 100 = 35%
Area of square ABCO is 169 and that of square EFGD is 49. Find area of quadrilateral FBCG.
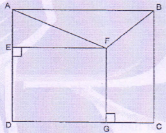
-
Solution

\(□\)FBCG is a trapezium as sides FG and BC are parallel.
\(□\)ABCD is a square.
∴ AB = BC = CD = DA = 13
\(□\) EFGD is also a square
∴ EF = FG = GD = ED = 7
EF + GC = 13 ∴ GC = 6
∴ Area of trapezium FBCG
= 1⁄2 x (13 + 7) × 6 = 60
The cost of a tennis racket is t⁄3 and that of tennis ball is b⁄7. What is the average (arithmetic mean) cost per unit of a collection of b units of tennis rackets and t units of tennis balls?
-
Solution
'b' tennis rackets cost \(\frac{bt}{3}\) and 't' tennis balls cost \(\frac{bt}{7}\).∴ The total cost of 'b' tennis rackets and 't'
tennis balls = \(\frac{bt}{3}+\frac{bt}{7}=\frac{10bt}{21}\)
∴ Average cost is \(\frac{\frac{10bt}{21}}{b+t}=\frac{10bt}{21(b+t)}\)
A train 100 meters long meets a man walking in opposite direction at the speed of 10 kmph and passes him in 71⁄5 seconds. What is the speed of the train?
-
Solution
While crossing the man train will cross its own length. Since the man is going in opposite direction the speed of crossing will be the speed of train plus the speed of man.
In 71⁄5 seconds train crosses 100 meters.
∴ In 3600 seconds, train crosses 50000 meters i.e. 50 kmph. is the combined "speed" of train and man.
Out of which speed of man is 10 kmph. ∴ Speed of train is 40 kmph.
Evaluate the sum 5√3 – 2\(\sqrt{12}\) – \(\sqrt{32}\) + \(\sqrt{50}\)
-
Solution
Denominator = 5√3 - 2\(\sqrt{12}\) -\(\sqrt{32}\) + \(\sqrt{50}\)
= 5√3 - 4√3 - 4√2 + 5√2 = √2 + √3
A rectangular lawn is made within a garden which is 20 ft. wide and 48 ft. long. Area of lawn is 3⁄4 of the area of garden. Dimensions of the lawn are in the same ratio as that of the garden. How many feet long is the lawn?
-
Solution
Area of rectangular garden = 20 × 48 = 960 ft
∴ Area pf lawn = 960 × 3⁄4 = 720 ft2
Ratio of dimensions of garden and lawn is \(\frac{20}{48}\) = 5 : 12
Let the dimensions of lawn be 5x and 12x respectively.
∴ 60 × 2 = 720 ∴ x = 2-√3
∴ Length of lawn = 12 × 2-√3 = 24-√3 ft.
Paul must choose 3 out of 5 shirts and 4 out of 6 trousers. How many different combinations are available to him?
-
Solution
3 shirts out of 5 can be chosen in 5C3 number of ways. 5C3 = \(\frac{5\times 4}{2}\) = 10 ways.
4 trousers of 6 can be chosen in 6C4 number of ways. 6C4 = 6C2 = \(\frac{6\times 5}{2}\) = 15 ways.
∴ Total number of combinations = 10 × 15 = 150
A distillate flows into an empty 96 gallon drum at spout P and out of drum at spout Q. If the rate of flow through P is 2 gallons per hour, how many gallons per hour must flow out at spout Q so that drum is full in exactly 144 hours?
-
Solution
Spout P and spout Q both are operating for 144 hours and a drum of 96 gallons is filled up completely.
Speed of spout P is 2 gallons per hour and spout Q is q gallons per hour.
(144 × 2)-(144 × q) = 96
∴ 144q = 192 ∴ q = \(\frac{192}{144}\) = 4⁄3 gallons per hr.
