GRE
Practice Test 32
Previous Solution Next

In how many ways can 2 vowels and 2 consonants from ‘THURSDAY’ be arranged?

  • Solution

    Answers:A,B,C,D

    Out of the letters of 'THURSDAY', 2 vowels can be picked in 2C2 ways and 2 consonants can be picked in 6C2 ways. The 4 letters can then be arranged in 4! ways no of ways of formations = 2C2 × 6C2 × 4!

    On solving this we get the other options

A person X speaks truth in 60% of cases and another person Y speaks truth in at least 75% of cases. In what percent of cases will an incident be correctly reported by both of them?

  • Solution

    Ans: A, D

    P(x) = 3⁄5 ⇒ Probability of x speaking truth,

    P(x) = \(\frac{75}{100}\) ⇒ Probability of x speaking truth,

    For both x and y to speak the truth, min probability is = (P(x) . P(y))

    = \(\left ( \frac{3}{5}\times \frac{3}{4} \right )=\frac{9}{20}\)= 45% or more

A man travels three-fifth of the distance at a speed of 3a and the remaining at a speed 2b. If he travels twice the distance at a speed of 5c he still requires same time. Then which of the following is false.

  • Solution

    Ans: A, B, D

    Let the distance between AB be X given

    Total distance traveled from A to B and back = 2x Speed = 5c

    ∴ Time taken = \(\frac{2x}{5c}\)

    But,\(\frac{x}{5a}+\frac{x}{5b}=\frac{2x}{5c}\Rightarrow \frac{1}{a}+\frac{1}{b}=\frac{2}{c}\)

    Hence c is harmonic mean of a and b, other options are false

ABC Corporation employed 600 men and 400 women. The average wage was S25.40 per day. Which of the following could be the wage of one man and the wage of one woman for one day?

  • Solution

    Ans: (B, C, E)

    Let the daily wage of man be $x and that of woman = $y

    ∴ 600x + 400y = 25.4 × (600 + 400)

    ∴ 600x + 400y = 25400

    ∴ 3x + 2y = 127

In an office, 3⁄5 of the employees can neither drive a car nor a two wheeler. However, 1⁄5 can drive only a car then which two statements will be sufficient to determine the total number of employees in the office?

Mark two correct options:

  • Solution

    Ans: (A, D)

    The information missing is the number of employees driving both and those driving only two wheelers.

    And the number of employees in anyone subset. Hence we require statements A and D

When one number is divided by second one, the quotient is 3 and remainder is 8. Find the numbers.

  • Solution

    Answer: (B, C)

    Let the smaller number be x.

    Then the larger number = 3x + 8

    But x > 8 since the remainder is always less than quotient

The taxi charges in Philadelphia comprise of a fixed charge, together with the charge of $x per km of the distance covered. For a journey of 16 km, charges paid are $156. If x is an integer, what is the possible value of the initial fixed charge?

  • Solution

    Answer: (B, C, E)

    Let the fixed charge be 'f and variable charge is x per km.

    Then, according to condition 1,

    f+ 16x = 156 (I)

    Hence 156 - f should be divisible by 16, since x is an integer.

If the function f(x) = X2 + 3x -10 is negative then which are the possible values of x:

  • Solution

    Answer: B, C, D

    The equation can be factorized as f(x) = (x - 5)(x + 2), If the answer has to be negative then x should be between -2 and 5, both exclusive

Distance between two places P and Q is 100 metres. Person A is at P and person B is at Q. Speeds of A and B are 20 metres per second and 30 metres per second respectively. They travel to and fro between P and Q. The total distance covered by A and B together is 1000 metres. Identify all possible times at which they meet;

  • Solution

    Options A, B, C, F

A pentagonal hall ABCDE is as shown in the figure with all the angle of the pentagon less than or equal to 180° and BC parallel to ED and AE parallel to CD. Which of following are the possible measures of the wall AB of the hall?

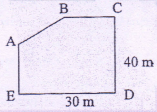
  • Solution

    Ans: (B, C, D)

    The minimum value of length of AB will be when BAE is straight line, then AB=40-20=20m and the value will be maximum when B coincides with C. Then

    AB = \(\sqrt{(30^{2} + 20^{2}) }\) = 31.62

    Hence AB should be between 20 and 31.62m hence the correct options are B, C and D

Attempted

0

Correct

0

Wrong

0

Complete
Problem solving
Attempted
Wrong
Correct