| \(\left ( 2-\frac{1}{3} \right )\left ( 2-\frac{3}{5} \right )\left ( 2-\frac{5}{7} \right )…..\left ( 2-\frac{999}{1001} \right )\) | 333 |
-
Solution
Col. A-
\(\frac{5}{3}\times \frac{7}{5}\times \frac{9}{7}......\frac{1003}{1001}\)
=\(\frac{1003}{3}> 334\)
| Probability that a three digit number chosen at 1 random is a palindrome | 1⁄9 |
-
Solution
There are 10 palindromes in each of hundreds from 100 to 900 i.e. 10 in 100 to 199, (101,111,121...191). Similarly 10 in 200 to 299 and so on.
∴ There are 90 palindromes in 900 nos.
Required probability is \(\frac{90}{900}=\frac{1}{10}\)
| 1053×258 | 1050×260 |
-
Solution
Follow the rule of taking minimum and minimum numbers together
Col. A (1050 × 258) + (3 × 258)
Col. B (1050 × 258) + (1050 × 2)
∴ Answer is B

| Area of shaded port on | 1.5 |
-
Solution
Col. A
ΔAB is tangent and therefore ∠OBA = 90°
∴ Area of ((∠OAB) =\(\frac{2\times 2\sqrt{3}}{2}\)= 2√3 ⇒ 3.4
Area of sector = πr2 × \(\frac{60}{360}=\frac{4\pi }{6}=\frac{2\pi }{3}\Rightarrow 2\)
∴ Area of ▪ portion 3.4 - 2 = 1.4
| \(\sqrt{35}-\sqrt{15}\) | \(\sqrt{35-15}\) |
-
Solution
Col. A-
\(\sqrt{35}-\sqrt{15}\Rightarrow \sqrt{36}-\sqrt{16}=2\)
Col. B-
\(\sqrt{20}=2\sqrt{5}\)
| HCF of 3⁄7 and 1⁄2 | LCM of 3⁄7 and 1⁄2 |
-
Solution
Col. A-
\(\frac{HCF\, of\, Numerators}{LCM\, of\, Denominators}=\frac{1}{77}\)
Col. B-
\(\frac{LCM\, of\, Numerators}{HCF\, of\, Denominators}=\frac{12}{1}\)
k is an integer
| Remainder when k2 + 6k + 4 is divided by 2. | 1 |
-
Solution
Col. A-
If k Is even, remainder is O.
If k is odd, k2 is odd, 6k is even and 4 is even.
∴ Total is odd. ∴ Remainder is 1
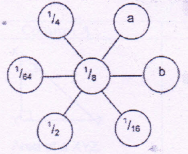
The number at the centre is the geometric mean of each pair of numbers diametrically opposite ends.
| a | b |
-
Solution
Col. A-
\(\frac{1}{64}\times b=\left ( \frac{1}{8} \right )\) ∴b=1
1⁄2 × a = (1⁄8)2 ∴ a =\(\frac{1}{32}\)
 |
In the correctly worked out division problem each of symbols \(□\) and Δ respresents a digit. |
| \(□\) | Δ |
-
Solution
319 × 67 ..... ends in 3 ∴ Δ = 3
\(□\) - 3 = 9 ∴ \(□\) = 12
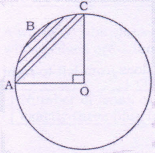
O is the center of circle.Area of triangle AOC = 8
| Area of the shaded portion | 6 |
-
Solution
Area of circle = πr2 = π(OA)2
ΔAOC is isosceles right angle triangle
∴ AO = OC = 16π
∴ Area of sector ABCO = = 4π
∴ Area of ▪ portion = 4π - 8 ≈ 4.56