| Arithmetic mean of a, b and c | a |
-
Solution
a - b = c - a :∴ 2a = b + c ∴ 3a = a + b + c
Required mean =\(\frac{a + b + c}{3}=\frac{3a}{3}\)= a
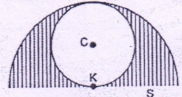
Circle with centre C is inscribed in a semicircle S, with centre K.
| Area of shaded region | Area of unshaded region |
-
Solution
Let radius of inscribed circle be 1
∴ Area = π12 which is area of unshaded region.
∴ Radius of semicircle = 2
∴ Area of semicircle = \(\frac{\pi 2^{2}}{2}\) = 2π
∴ Area of shaded region = 2π - π = π
After 1⁄4 of passengers leave, remaining passengers use only 2 of the buses
| Fraction of seats on the 2 buses that are now occupied | \(\frac{9}{10}\) |
-
Solution
Let there be 5 seats on each bus.
∴ Total seats = 15
Occupied 4 seats = 4⁄5 × 15 = 12
After 1⁄4 of them get off, 9 passengers will travel.
Two busses will have total of 10 seats.
∴ Required fraction = \(\frac{9}{10}\)
| Total number of different positive 3 digit numbers where arithmetic mean of three digits is equal to 2 | 20 |
-
Solution
Average is 2 ⇒ sum of 3 digits must be 6.
There are 6 nos. between 100 and 200.
105,114,123,132,141,150
200 to 300 → 204, 213, 222, 231, 240
300 to 400 → 303, 312, 321, 330
400 to 500 → 402,411,420
500 to 600 → 501,510
600 to 700 → 600
∴ Total numbers 6 + 5 + 4 + 3 + 2 + 1 = 21

| R⁄r | 1.5 |
-
Solution
Area of unshaded region = πr2
Area of shaded region = πR2 - πr2 = π(R2 - r2)
∴ π(R2 - r2) = πr2
∴ R2 = 2r2 ∴ R⁄r= √2 = 1.414
| Arithmetic mean of a and b | Arithmetic mean of a, b, b |
-
Solution
Average of a and b = \(\frac{a+b}{2}\)
∴ Addition of one more b will raise the average as b > a
The problem can also be attempted by plugging in nos. such as a = 2, b = 3.
q < p
| Remainder when q is divided by p | Remainder when p is divided by q |
-
Solution
Col. A-
When q is divided by p, quotient is zero and remainder is q.
Col. B-
When p is divided by q, the remainder r is always less than the divisor q.

| Length of QR | 7 |
-
Solution
If x = 90°, then PQ = PR = 5 and QR = 5√2 = (5 × 1.414) > 7
Since X > 90°, QR > 5 √2 > 7
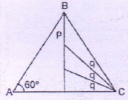
| p + q | 50 |
-
Solution
Since we do not know measurement of p and q, it is not possible to find out the answer.
2c – 3b = 6d
| Arithmetic mean of a, b, c, d | 3d |
-
Solution
Adding the two equations
2a + 2b + 2c= 18d
∴ a + b + C = 9d
∴ a + b + C + d = 10d
∴ \(\frac{a + b + c + d}{4}\) = 2. 5d ⇒ Col. A
If d is negative answer will be B.
∴ The actual answer should be D.