| Number of students playing tennis | Number of students not playing tennis |
-
Solution
More than half the no. of boys and girls play tennis. Therefore column A is greater.
m + n = 12
| m | 8 |
-
Solution
The only prime numbers whose sum is 12 are 5 and 7, both of which are less than 8.
Note that 1+11 =12 but 1 is not prime numbers.
| r4 – r3 + r2 – r | r – r2 + r3 – r4 |
-
Solution
Col. B = -1 × Col. A
∴ Col. A= 16 + 8 + 4 + 2 = 30
∴ Col. B = -30
| q-p | 6 |
-
Solution
By distance formula
10 = \(\sqrt{(q-p)^{2}+(-3-5)^{2}}\)
∴ 100 = (q - p)2 + 64 ∴ q - p = 6
a > b > 0 > C > d
| a + c | b + d |
-
Solution
Compare the columns piece by piece. Note that a and b are positive and c and d are negative. Also a > b and C > d.
∴ a + c > b + d
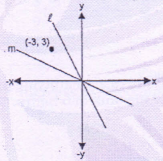
| Slope of line m | Slope of line ℓ |
-
Solution
Line passing through (-3, 3) and (0, 0) has slope -1. Line ℓ is steeper, so its slope is -2, -3, -4....
Line m is less steeper. So its slope could be -0.2, -0.1, -0.01...
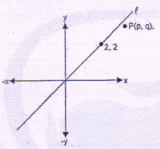
| p – q | O |
-
Solution
Line ℓ which pastes through origin and (2, 2) also passes through point (p, p). Since P(p, q) is below line ℓ, q < p.
| S2 | 1 |
-
Solution
If the sides of the square are exactly horizontal and vertical, then S = 1 or -1. However, the square could be positioned in any place and so the slope of the diagonal could be any no. Example -

| Value of x2 + 6x + 9 When x = 43.9 | Value of x2 – 6x + 9 When x = 49.9 |
-
Solution
Col. A-
X2 = 6x + 9 = (x + 3)2
∴ Value required = (43.9 + 3)2 = (46.9)2
Col. B-
X2 - 6x + 9 = (x - 3)2
∴ Value required = (49.9 - 3)2 = (46.9)2
| The number of rades over 80 | 5 |
-
Solution
For the average to be 80, it is not. mandatory to have exactly 5 nos. above 80 and 5 below 80.
In fact. All we can say is that there should be atleast one grade above 80 or atleast one below 80.
