If line CD is 25 units from line AB, and the measure of angle IKD is 135°, what is the length of line segment IK?
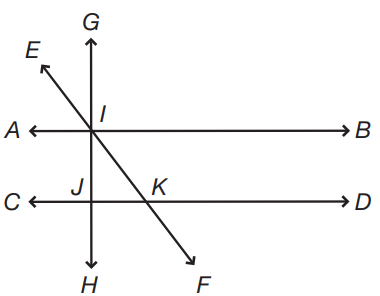
Line AB is parallel to line CD, and line GH is perpendicular to lines AB and CD. The diagram is not to scale.
-
Solution
Since angle IKD is 135°, and it is supplementary to angle IKJ, the measure of angle IKJ = 180 – 135 = 45. Lines GH and CD form a right angle, IJK, since these lines are perpendicular. Since angle IKJ = 45°, angle JIK is also 45° (180 – (90 + 45) = 45). Therefore, triangle IJK is an isosceles right triangle. The length of side IJ is 25 units, since line CD is 25 units from line AB. The hypotenuse of an isosceles right triangle is equal to √2 times the length of a base. Since the length of a base, IJ, is 25, the hypotenuse, IK, is 25√2 units.
If line segment JK is 16 units long, what is the length of line segment IK?

Line AB is parallel to line CD, and line GH is perpendicular to lines AB and CD. The diagram is not to scale.
-
Solution
To find the hypotenuse of a right triangle, you must add the squares of the base lengths. However, only the length of one base is given. There is no information provided about the angles of triangle IJK, so you cannot determine if this is a certain type of right triangle. Therefore, the length of side IK cannot be determined from the information provided.
Angle Q of triangle PQR is a right angle, and side QR measures 4 units. If the sine of angle P is equal to the sine of angle R, what is the length of side PR?
-
Solution
If angle Q is the right angle of the triangle, then side QR is a base of the right triangle. If the sine of P is equal to the sine of R, then angle P is equal to angle R. Therefore, PQR is an isosceles right triangle. The hypotenuse of an isosceles right triangle is equal to √2 times the length of a base. Since the length of a base is 4, the hypotenuse of the triangle is 4√2 units.
The hypotenuse of an isosceles right triangle measures x units. What is the length of a base of the triangle?
-
Solution
The hypotenuse of an isosceles right triangle is equal to √2 times the length of a base, and the base of the triangle is equal to \(\frac{\sqrt{2}}{2}\) times the length of the hypotenuse. Since the hypotenuse of the triangle is x, the bases of the triangle each measure \(\frac{\sqrt{2}}{2}\) units.
Angle T of right triangle TUV measures 45°. If base TU measures 10 units, what is the length of the hypotenuse of triangle TUV?
-
Solution
If the measure of one base angle of a right triangle is 45°, then the measure of the other base angle must also be 45° (180 – (90 + 45) = 45). Therefore, TUV is an isosceles right triangle, or a 45-45-90 right triangle. The hypotenuse of a 45-45-90 right triangle is equal to √2 times the length of a base. Since the length of a base is 10, the hypotenuse of the triangle is 10√2 units.
Which of the following triangles is a multiple of the triangle with sides measuring x, x – 5, and x + 5, when x is greater than 0?
-
Solution
The hypotenuse of the given triangle is x + 5, since x cannot be 0 or negative (the side of a triangle cannot be 0 or negative); therefore, x + 5 > x > x – 5. Using the Pythagorean theorem, (x)2 + (x – 5)2 = (x + 5)2; x2 + x2 – 10x + 25 = x2 + 10x + 25, 2x2 – 10x + 25 = x2 + 10x + 25, x2 – 20x = 0, x(x – 20) = 0, and x = 20, since x cannot be 0. Therefore, the sides of the triangle measure 20, 20 – 5 = 15, and 20 + 5 = 25. The sides of the triangle, 15, 20, 25, are a multiple of the triangle with sides 3, 4, 5, since 3(5) = 15, 4(5) = 20, and 5(5) = 25
If the longer base of triangle XYZ is three times the length of the shorter base, a, what is the length of the hypotenuse in terms of the shorter base?
-
Solution
If the shorter base is a, then the longer base is 3a. Use the Pythagorean theorem: a2 + (3a)2 = c2, a2 + 9a2 = c2, 10a2 = c2, c = a\(\sqrt{10}\).
If the lengths of the bases of right triangle GHI are 9 units and 15 units respectively, what is length of the hypotenuse of triangle GHI?
-
Solution
Use the Pythagorean theorem: 92 + 152 = x2, 81 + 225 = x2, x2 = \(\sqrt{306}\), x = 306 = \(\sqrt{306}\).
If the length of a base of right triangle DEF is 8 units and the hypotenuse of triangle DEF is 8√5 units, what is the length of the other base?
-
Solution
Use the Pythagorean theorem: 82 + x2 = (8√5)2, 64 + x2 = 320, x2 = 256, x = 16 (x cannot equal –16 since the side of a triangle cannot be negative).
The bases of a right triangle measure x – 3 and x + 4. If the hypotenuse of the triangle is 2x – 3, what is the length of the hypotenuse?
-
Solution
Use the Pythagorean theorem: (x – 3)2 + (x + 4)2= (2x – 3)2, x2 – 6x + 9 + x2 + 8x + 16 = 4x2 – 12x + 9, 2x2 + 2x + 25 = 4x2 – 12x + 9, 2x2 – 14x – 16 = 0, x2 – 7x – 8 = 0, (x – 8)(x + 1) = 0, x = 8. Disregard the negative value of x, since a side of a triangle cannot be negative. Since x = 8, the length of the hypotenuse is 2(8) – 3 = 16 – 3 = 13.