If the sum of the interior angles of a regular polygon equals 720°, and the length of one side of the polygon is 3x2, what is the perimeter of the polygon?
-
Solution
The sum of the interior angles of a polygon is equal to 180(s – 2), where s is the number of sides of the polygon; 720 = 180(s – 2), 720 = 180s – 360, 1,080 = 180s, 108 = 18s, s = 6. Since the polygon is regular, has 6 sides, and the length of one side is 3x2, the perimeter of the polygon is 6(3x2) = 18x2 units.
What is the perimeter of an isosceles right triangle whose hypotenuse is 5√2 units?
-
Solution
The hypotenuse of an isosceles right triangle is equal to √2 times the length of a base of the triangle. If the hypotenuse is 5√2, then the length of each base is \(\frac{(5\sqrt{2})}{(\sqrt{2})}\) = 5. Therefore, the perimeter of the triangle is 5 + 5 + 5√2 = 10 + 5√2 units.
The ratio of the lengths of a side of regular pentagon ABCDE to the length of a side of regular hexagon PQRSTU is 5:6. If the perimeter of pentagon ABCDE is 75 units, what is the perimeter of hexagon PQRSTU?
-
Solution
If the perimeter of a regular pentagon is 75 units, then the length of one side of the pentagon is \(\frac{75}{5}\) = 15 units. The ratio of a length of ABCDE to a length of PQRSTU is 5:6. Therefore, if x is the length of a side of PQRSTU, then 5⁄6 = \(\frac{15}{x}\), 5x = 90, and x = 18 units. Since the length of one side of the regular hexagon is 18, the perimeter of the hexagon is (6)(18) = 108 units.
The perimeter of a regular seven-sided polygon is 11x – 4. If x = 8, what is the length of one side of the polygon?
-
Solution
If x = 8, then the perimeter of the figure is 11(8) – 4 = 88 – 4 = 84. Every side of a regular polygon is equal in length. Therefore, the length of one side of this seven-sided polygon is \(\frac{84}{7}\) = 12 units.
If the perimeter of the figure below is 60 units, what is the length of \(\overline{BC}\)?
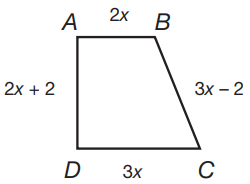
-
Solution
The perimeter of ABCD is equal to the sum of its sides: 2x + 2x + 2 + 3x + 3x – 2 = 60, 10x = 60, x = 6. Therefore, the length of \(\overline{BC}\) is 3(6) – 2 = 18 – 2 = 16 units.