If the radius of the circle is 9 units, what is the length of arc DB?
The diagram is not to scale.
-
Solution
The length of an arc is equal to the circumference of the circle multiplied by the fraction of the circle that the arc covers. The circumference of the circle is equal to (2π)(9) = 18π units. The central angle of arc DB is 40°, which means that the length of the arc is \(\frac{40}{360}\) of the circumference of the circle: \(\frac{40}{360}\)(18π) =1⁄9(18π) = 2π units.
If the radius of the circle is 27 units, what is the length of arc AE?
The diagram is not to scale.
-
Solution
The length of an arc is equal to the circumference of the circle multiplied by the fraction of the circle that the arc covers. The circumference of the circle is equal to (2π)(27) = 54π units. The central angle of arc AE is 80°, which means that the length of the arc is \(\frac{80}{360}\) of the circumference of the circle: \(\frac{80}{360}\) (54π) = 2⁄9(54π) = 12π units.
If the radius of the circle is 15 units, what is the area of sector DOB?
The diagram is not to scale.
-
Solution
The area of a sector is equal to the area of the circle multiplied by the fraction of the circle that the sector covers. The area of the circle is equal to π(152) = 225π. Since the angle of the sector is 40°, \(\frac{40}{360}\)(225π) = 1⁄9 (225π) = 25π square units.
If the radius of the circle above is 12 units, which sector has an area of 24π square units?
The diagram is not to scale.
-
Solution
The area of a sector is equal to the area of the circle multiplied by the fraction of the circle that the sector covers. The area of the circle is equal to π(122) = 144π. If the area of the sector is equal to 24π, and the angle of the sector is x, then \(\frac{x}{360}\)(144π) = 24,\(\frac{x}{360}\) = 24π, 2x = 120, x = 60. Angle EOD is 60°; therefore, sector EOD is the sector with an area of 24π square units.
If the length of \(\overline{OA}\) is 8 units and the measure of angle AOC is 50°, what is the area of sector AOC?
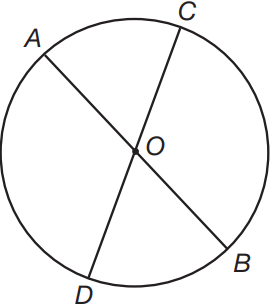
The diagram is not to scale.
-
Solution
The area of a circle is equal to πr2. The area of this circle is π(8)2 = 64π square units. The area of the sector is equal to a fraction of that: \(\frac{50}{360}\)(64π) = \(\frac{50}{360}\)(64π) = \(\frac{50}{360}\)(16π) = \(\frac{50}{360}\)π square units.
If the area of the circle is 196π square units, what is the length of \(\overline{CD}\)?
The diagram is not to scale.
-
Solution
The area of a circle is equal to πr2; πr2 = 196π, r2 = 196, r = 14. \(\overline{CD}\) is a line from one side of the circle, through the center of the circle, to the other side of the circle. It is a diameter, and the measure of a diameter is twice the measure of a radius. The measure of line CD is (2)(14) = 28 units.
If the length of \(\overline{OD}\) is 6 units and the measure of angle COB is 100°, what is the length of arc CB?
The diagram is not to scale.
-
Solution
The length of arc CB is equal to the size of central angle COB divided by 360, multiplied by the circumference of the circle. Since the radius of the circle is 6 units, the circumference of the circle is 12π;\(\frac{100}{360}\)(12π) = \(\frac{100}{360}\)(12π) =\(\frac{10}{3}\)π units.
If the measure of angle AOC is 60°, what is the measure of arc DB?
The diagram is not to scale.
-
Solution
Angles AOC and DOB are vertical angles; their measures are equal. Therefore, angle DOB is also 60°. The intercepted arc of a central angle is equal in measure to the central angle. Arc DB measures 60°.
If the length of \(\overline{AO}\) is 15 units, what is the circumference of the circle?
The diagram is not to scale.
-
Solution
The circumference of a circle is equal to 2πr, where r is the radius of the circle. Therefore, the circumference of this circle is equal to (2π)(15) = 30π units.