If the radius of the circle is 4 units, what is the size of the shaded area?
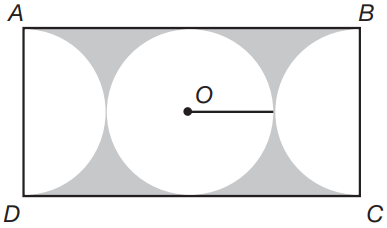
The semicircles to the left and right of the center circle are each exactly half the size of the center circle, and the three figures are adjacent within rectangle ABCD. The diagram is not to scale.
-
Solution
The area of the circle is equal to 16π square units, since the area of a circle is equal to πr2, where r is the radius of the circle. The length of \(\overline{AB}\) is equal to the length of four radii of the circle placed end to end. Therefore, the length of \(\overline{AB}\) is 4(4) = 16 units. Since \(\overline{BC}\) is the length of two radii, its length is 2(4) = 8 units. The area of a rectangle is lw, where l is the length of the rectangle and w is the width of the rectangle. The area of this rectangle is (16)(8) = 128 square units. There is one whole circle and two half circles within the rectangle—a total of 2 circles. Subtract the area of the circles from the area of the rectangle to find the size of the shaded area: 128 – 2(16π) = 128 – 32π square units.
If the area of one semicircle is 4.5π square units, what is the area of the rectangle?

The semicircles to the left and right of the center circle are each exactly half the size of the center circle, and the three figures are adjacent within rectangle ABCD. The diagram is not to scale.
-
Solution
If the area of one semicircle is 4.5π square units, then the area of a whole circle is 2(4.5π) = 9π square units. Since the area of a circle is equal to πr2, where r is the radius of the circle, the radius of the circle is equal to √9 = 3 units. Since the length of \(\overline{BC}\) is the length of 2 radii, the length of \(\overline{BC}\) is 2(3) = 6 units. The length of \(\overline{AB}\) is the length of 4 radii, or 4(3) = 12 units. The area of a rectangle is lw, where l is the length of the rectangle and w is the width of the rectangle. The area of this rectangle is (12)(6) = 72 square units.
If the length of \(\overline{AB}\) is x units, what is the area of the center circle?

The semicircles to the left and right of the center circle are each exactly half the size of the center circle, and the three figures are adjacent within rectangle ABCD. The diagram is not to scale.
-
Solution
The length of \(\overline{AB}\) is equal to the length of 4 radii of the center circle. Therefore, the radius of the center circle is x⁄4. Since the area of a circle is equal to πr2, where r is the radius of the circle, the area of the circle is equal to π(x⁄4)2 = \(\frac{\left (x^{2}\pi \right )}{16}\) square units.
If the area of the square is 144 square units, what is the total area of the figure?
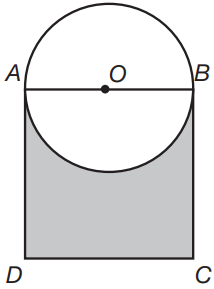
ABCD is a square. The diagram is not to scale.
-
Solution
If the area of the square is 144 square units, then the area of one side of the square is \(\sqrt{144}\) = 12 units. Since a side of the square is equal to the diameter of the circle, the diameter is 12 units and the radius of the circle is 6 units. The area of the circle is 62π = 36π square units. The total area of the figure is equal to the area of the square plus half the area of the circle (since the other half of the circle is within the area of the square): 144 + (\(\frac{36\pi }{2}\)) = 144 + 18π square units.
If the area of the circle is 8x2π, what is the size of the shaded area?

ABCD is a square. The diagram is not to scale.
-
Solution
If the area of the circle is 8x2π, then the radius of the circle is 2x√2, since the area of a circle is equal to πr2, where r is the radius of the circle. If the radius of the circle is 2x√2, then the diameter of the circle, and the length of a side of the square, is 2(2x√2) = 4x√2. The area of a square is equal to the length of one of its sides squared. Therefore, the area of this square is equal to (4x√2)2 = 32x2. The shaded area is equal to the area of the square minus half the area of the circle: 32x2 –\(\frac{(8x^{2}\pi )}{2}\) = 32x2 – 4x2π.
If the area of the circle is 25π cm2, what is the length of diagonal AD?
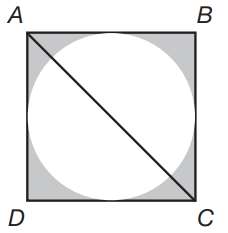
The diagram is not to scale.
-
Solution
If the area of the circle is 25π cm2, then the radius of the circle is 5 cm, since the area of a circle is equal to πr2, where r is the radius of the circle. If the radius of the circle is 5 cm, then the diameter of the circle, and the length of a side of the square, is 2(5) = 10 cm. The diagonal of a square is √2 times the length of one of its sides. Therefore, the length of diagonal AD is 10√2 cm.
If the length of \(\overline{BD}\) in square ABCD is x ft., what is the size of the shaded area?

The diagram is not to scale.
-
Solution
The area of a square is equal to the length of one of its sides squared. Therefore, the area of the square is x2 ft.2. The diameter of the circle is equal to the length of a side of the square, x, which means that the radius of the circle is equal to 1⁄2(x) ft. The area of a circle is equal to πr2, where r is the radius of the circle. The area of this circle is equal to (1⁄2(x))2π= (\(\frac{x^{2}}{4}\))π ft.2. The shaded area is the difference between the area of the square and the area of the circle: x2 – (x⁄4)π = x2 – 1⁄4 (x)1⁄2(π) ft.1⁄2.
If \(\overline{OF}\) = \(\overline{FB}\), angle D = angle B, the radius of the circle is 6x and arc EF is 60°, what is the perimeter of triangle DOB?
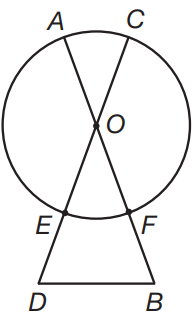
The diagram is not to scale.
-
Solution
The measure of central angle DOB is 60°, since the measure of its intercepted arc, EF, is 60°. There are 180° in a triangle, which means that the sum of angles D and B is 180 – 60 = 120. Since these angles are equal, each angle measures \(\frac{120}{2}\) = 60°. Since every angle in the triangle measures 60°, DOB is an equilateral triangle. The radius of the circle is 6x.\(\overline{OF}\) is a radius of the circle, and it is equal in length to FB. Therefore, the length of side OB of triangle DOB is 2(6x) = 12x. Since this is an equilateral triangle, all three sides of the triangle measure 12x. The perimeter of the triangle is 12x + 12x + 12x = 36x.
If angles D and B both equal 70°, what is the measure of arc AC?

The diagram is not to scale.
-
Solution
If angles D and B are 70°, then angle DOB is equal to 180 – (70 + 70) = 180 – 140 = 40°, since there are 180° in a triangle. Angles DOB and AOC are vertical angles; their measures are equal. Since angle AOC is also 40°, and the measure of an intercepted arc of a central angle is equal to the measure of the central angle, arc AC also measures 40°.
The circumference of a circle is 16π cm. What is the area of a sector whose central angle measures 120°?
-
Solution
The circumference of a circle is 2πr, where r is the radius of the circle, so the radius of this circle is \(\frac{16\pi }{2\pi }\) = 8 cm. The area of a circle is equal to πr2, so the area of this circle is (8)2π = 64π cm2. The area of a sector is equal to the area of the circle multiplied by the fraction of the circle that the sector covers. That fraction is equal to \(\frac{120}{360}\),so the area of the sector is equal to \(\frac{120}{360}\)(64π) = 1⁄3(64π) = \(\frac{64}{3}\)π cm2.