Of the equations graphed on the coordinate planes, which function has the smallest range?
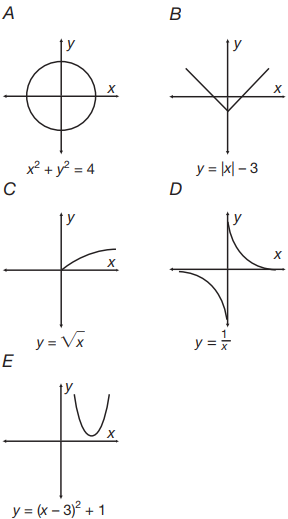
-
Solution
The graph of the equation in diagram A is not a function. It fails the vertical line test for all x values where –2 < x < 2. The equation of the graph in diagram B is y = |x| – 3. Any x value greater than or less than 3 will generate a y value that is greater than –3; no values less than –3 can be generated by this equation. Therefore, the range of the equation y = |x| – 3 is all real numbers greater than or equal to –3. The equation of the graph in diagram C is y = x. Since the square roots of negative numbers are imaginary, the range of this equation is all real numbers greater than or equal to 0. The equation of the graph in diagram D is y = 1⁄x. One divided by a real number (excluding 0) will yield real numbers, excluding 0. There is no value for x that can make y = 0. Therefore, the range of the equation y = 1⁄x is all real numbers excluding 0. The equation of the graph in diagram E is y = (x – 3)2 + 1. Any x value greater than or less than 3 will generate a y value that is greater than 1; no values less than 1 can be generated by this equation. Therefore, the range of the equation y = (x – 3)2 + 1 is all real numbers greater than or equal to 1. Of the four equations that are functions, the equation y = (x – 3)2 + 1 (E), has the smallest range (fewest elements), since the set of real numbers that are greater than or equal to 1 is smaller than the set of all real numbers greater than or equal to –3 (B), smaller than the set of all real numbers greater than or equal to 0 (C), and smaller than the set of all real numbers excluding 0 (D).
Which of the coordinate planes shows the graph of a function that has the same range as its domain?
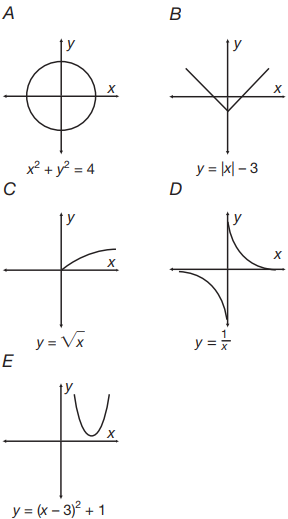
-
Solution
The equation of the graph in diagram C is y = x. Since the square root of a negative number is imaginary, the domain of this equation is all real numbers greater than or equal to 0. The square roots of real numbers greater than or equal to 0 are also real numbers that are greater than or equal to 0. Therefore, the range of the equation y = √x is all real numbers greater than 0, and the domain and range of the equation are the same. The equation of the graph in diagram D is y = 1⁄x. If x = 0, this function will be undefined. Therefore, the domain of this function is all real numbers excluding 0. One divided by a real number (excluding 0) will yield real numbers, excluding 0. Therefore, the range of the equation y = 1⁄x is all real numbers excluding 0, and the domain and range of the equation are the same. The equation of the graph in diagram B is y = |x| – 3. Any real number can be substituted into this equation. There are no x values that will generate an undefined or imaginary y value. However, it is impossible to generate a y value that is less than –3. Any x value greater than or less than 3 will generate a y value that is greater than –3. Therefore, the range of the equation y = |x| – 3 is all real numbers greater than or equal to –3. The domain and range of y = |x| – 3 are not the same. The equation of the graph in diagram E is y = (x – 3)2 + 1. With this equation as well, any real number can be substituted for x—there are no x values that will generate an undefined or imaginary y value. However, it is impossible to generate a y value that is less than 1. Any x value greater than or less than 3 will generate a y value that is greater than 1. Therefore, the range of the equation y = (x – 3)2 + 1 is all real numbers greater than or equal to 1. The domain and range of y = (x – 3)2 + 1 are not the same.
Which of the coordinate planes shows the graph of a function that has a domain of all real numbers?
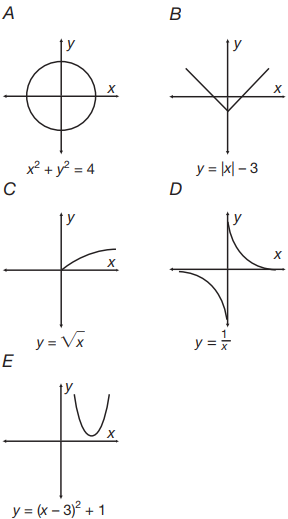
-
Solution
The equation of the graph in diagram B is y = |x| – 3. Any real number can be substituted into this equation. There are no x values that will generate an undefined or imaginary y value. The equation of the graph in diagram E is y = (x – 3)2 + 1.With this equation as well, any real number can be substituted for x—there are no x values that will generate an undefined or imaginary y value. The equation of the graph in diagram D is y = 1⁄x. If x = 0, this function will be undefined. Therefore, the domain of this function is all real numbers excluding 0. Only the functions in diagrams B and E have a domain of all real numbers with no exclusions.
Which of the coordinate planes shows the graph of a function that has a range that contains negative values?
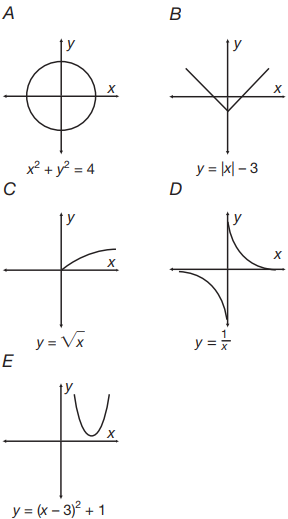
-
Solution
The range of a function is the set of possible outputs of the function. In each of the five equations, the set of possible y values that can be generated for the equation is the range of the equation. Find the coordinate planes that show a graph that extends below the x-axis. These equations have negative y values, which means that the range of the equation contains negative values. The graphs of the equations in diagrams A, B, and D extend below the x-axis. However, the graph of the equation in diagram A is not a function. It fails the vertical line test for all x values where –2 < x < 2. The equations graphed in diagrams B and D are functions whose ranges contain negative values.
Which of the coordinate planes shows the graph of an equation that is not a function?
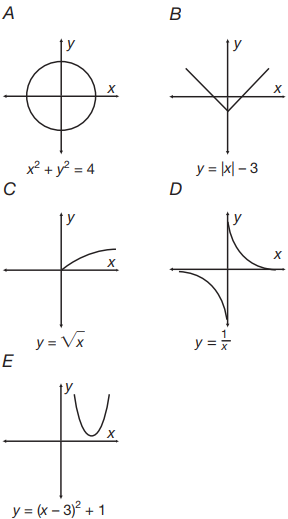
-
Solution
The graph of the equation in diagram A is not a function. A function is an equation in which each unique input yields no more than one output. The equation in diagram A fails the vertical line test for all x values where –2 < x < 2. For each of these x values (inputs), there are two y values (outputs).