(x2 – 3)(- 3x2 + 5)
Which of the following expressions is equivalent to the one above?
-
Solution
Applying the distributive property, the given expression can be rewritten as x2 − 3 + 3x2 − 5. Combining like terms yields 4x2 − 8.
Choice B is incorrect and is the result of disregarding the negative sign in front of the first 3 before combining like terms. Choice C is incorrect and is the result of not multiplying −3x2 by −1 before combining like terms. Choice D is incorrect and is the result of disregarding the negative sign in front of the first 3 and not multiplying −3x2 by −1 before combining like terms.
Feeding Information for Boarded Pets
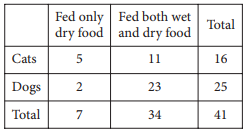
The table above shows the kinds of foods that are fed to the cats and dogs currently boarded at a pet care facility. What fraction of the dogs are fed only dry food?
-
Solution
There are 2 dogs that are fed only dry food and a total of 25 dogs. Therefore, the fraction of dogs fed only dry food is \(\frac{2}{25}\).
Choice A is incorrect. This fraction is the number of dogs fed only dry food divided by the total number of pets instead of the total number of dogs. Choice C is incorrect because it is the fraction of all pets fed only dry food. Choice D is incorrect. This fraction is the number of dogs fed only dry food divided by the total number of pets fed only dry food.
refer to the following information.
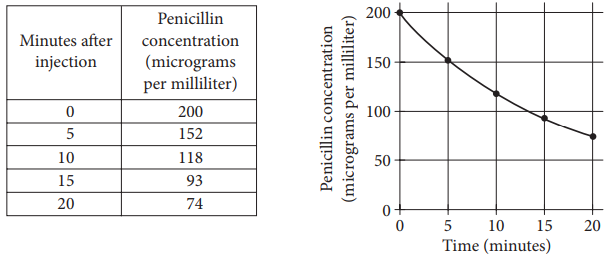
When a patient receives a penicillin injection, the kidneys begin removing the penicillin from the body. The table and graph above show the penicillin concentration in a patient’s bloodstream at 5-minute intervals for the 20 minutes immediately following a one-time penicillin injection.
The penicillin concentration, in micrograms per milliliter, in the patient’s bloodstream t minutes after the penicillin injection is modeled by the function P defined by P(t) = 200bt⁄5.If P approximates the values in the table to within 10 micrograms per milliliter, what is the value of b, rounded to the nearest tenth?
-
Solution
The correct answer is 0.8. The value of b in the equation P (t) = 200bt⁄5 can be estimated using any row of the table other than the first one. Substituting t = 5 and P (5) = 152 from the second row of the table into the definition of P yields 152 = 200b5⁄5, or 152 = 200b. Dividing both sides of this equation by 200 yields b = \(\frac{152}{200}\). The fraction can be rewritten as \(\frac{76}{100}\), or its decimal equivalent .76. Rounded to the nearest tenth, this value is .8. Other rows of the table also give a value of b that rounds to .8. Therefore, the value of b, rounded to the nearest tenth, is .8. Either .8, or its fractional equivalents, 4/5 or 8/10, can be gridded
as the correct answer.
refer to the following information.

When a patient receives a penicillin injection, the kidneys begin removing the penicillin from the body. The table and graph above show the penicillin concentration in a patient’s bloodstream at 5-minute intervals for the 20 minutes immediately following a one-time penicillin injection.
According to the table, how many more micrograms of penicillin are present in 10 milliliters of blood drawn from the patient 5 minutes after the injection than are present in 8 milliliters of blood drawn 10 minutes after the injection?
-
Solution
The correct answer is 576. According to the table, 5 minutes after the injection, the penicillin in the patient’s bloodstream is 152 micrograms per milliliter. Thus, there are 10 × 152 = 1520 micrograms of penicillin in 10 milliliters of blood drawn 5 minutes after the injection. Similarly, 10 minutes after the injection, the penicillin concentration is 118 micrograms per milliliter. Thus, there are 8 × 118 = 944 micrograms of penicillin in 8 milliliters of blood drawn 10 minutes after the injection. Therefore, there are 1520 − 944 = 576 more micrograms of penicillin in 10 milliliters of blood drawn 5 minutes after the injection than in 8 milliliters of blood drawn 10 minutes after the injection.
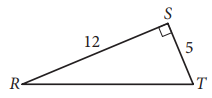
In triangle RST above, point W (not shown) lies on \(\overline{RT}\). What is the value of cos(∠RSW) − sin(∠WST) ?
-
Solution
The correct answer is 0. Note that no matter where point W is on \(\overline{RT}\), the sum of the measures of ∠RSW and ∠WST is equal to the measure of ∠RST, which is 90°. Thus, ∠RSW and ∠WST are complementary angles. Since the cosine of an angle is equal to the sine of its complementary angle, cos(∠RSW) = sin(∠WST). Therefore, cos(∠RSW) − sin(∠WST) = 0.
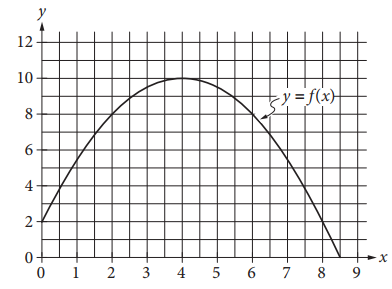
The graph of the function f, defined by f(x) x = − 1⁄2(x − 4)2 + 10, is shown in the xy-plane above. If the function g (not shown) is defined by g(x) = −x + 10, what is one possible value of a such that f(a) = g(a)?
-
Solution
The correct answers are 2 and 8. Substituting x = a in the definitions for f and g gives f(a) = −1⁄2 (a − 4)2 + 10 and g(a) = −a + 10, respectively. If f(a) = g(a), then −1⁄2(a − 4)2 + 10 = −a + 10. Subtracting 10 from both sides of this equation gives −1⁄2(a − 4)2 = −a. Multiplying both sides by −2 gives (a − 4)2 = 2a. Expanding (a − 4)2 gives a2 − 8a + 16 = 2a. Combining the like terms on one side of the equation gives a2 − 10a + 16 = 0. One way to solve this equation is to factor a2 − 10a + 16 by identifying two numbers with a sum of −10 and a product of 16. These numbers are −2 and −8, so the quadratic equation can be factored as (a − 2)(a − 8) = 0. Therefore, the possible values of a are either 2 or 8. Either 2 or 8 will be scored as a correct answer.
Alternate approach: Graphically, the condition f(a) = g(a) implies the graphs of the functions y = f(x) and y = g(x) intersect at x = a. The graph y = f(x) is given, and the graph of y = g(x) may be sketched as a line with y-intercept 10 and a slope of −1 (taking care to note the different scales on each axis). These two graphs intersect at x = 2 and x = 8.
On April 18, 1775, Paul Revere set off on his midnight ride from Charlestown to Lexington. If he had ridden straight to Lexington without stopping, he would have traveled 11 miles in 26 minutes. In such a ride, what would the average speed of his horse have been, to the nearest tenth of a mile per hour?
-
Solution
The correct answer is 25.4. The average speed is the total distance divided by the total time. The total distance is 11 miles and the total time is 26 minutes. Thus, the average speed is \(\frac{11}{26}\) miles per minute. The question asks for the average speed in miles per hour, and there are 60 minutes in an hour; converting miles per minute to miles per hour gives the following:
Average speed = \(\frac{11\, miles}{26\, minutes}\times \frac{60\, minutes}{1\, hour}\)
= \(\frac{660}{26}\) miles per hour
≈ 25.38 miles per hour
Therefore, to the nearest tenth of a mile per hour, the average speed of Paul Revere’s ride would have been 25.4 miles per hour.
In the xy-plane, the equations x + 2 = 10 y and 3 +6 = x y c represent the same line for some constant c. What is the value of c ?
-
Solution
The correct answer is 30.Since the equations x + 2y = 10 and 3x + 6y = c represent the same line in the xy-plane, they must be equivalent equations. The expression 3x + 6y on the left-hand side of the second equation is equivalent to 3(x + 2y), which is 3 times the left hand side of the first equation. Thus, to be equivalent, the right-hand side of the second equation, c, must be 3 times the right-hand side of the first equation, 10. Therefore, c = 30.
x − 1⁄2a = 0
If x = 1 in the equation above, what is the value of a ?
-
Solution
The correct answer is 2. Substituting x = 1 in the equation x − 1⁄2 a = 0 gives 1 − 1⁄2 a = 0. Adding 1⁄2 a to both sides of this equation gives 1 = 1⁄2 a. Multiplying both sides of this last equation by 2 gives 2 = a.
There are two atoms of hydrogen and one atom of oxygen in one molecule of water. How many atoms of hydrogen are there in 51 molecules of water?
-
Solution
The correct answer is 102. Since each molecule of water has 2 atoms of hydrogen, 51 molecules of water have a total of (51)(2) = 102 atoms of hydrogen