If the tangent of angle A is 0.75 and the measure of side AB is 4 less than the measure of side AC, what is the length of side BC?

The diagram is not to scale.
-
Solution
The tangent of angle A is equal to 0.75, or 3⁄4. Since the tangent of A is the measure of side BC divided by side AB, the ratio of side BC to side AB is 3:4. To find the relative length of side AC, use the Pythagorean theorem: 32 + 42 = (\(\overline{AC}\))2, 9 + 16 = (\(\overline{AC}\))2, 25 = (\(\overline{AC}\))2, \(\overline{AC}\) = 5. The ratio of side BC to side AB to side AC is 3:4:5. Since the length of side AB is 4 less, not 1 less, than the length of side AC, multiply each number in the ratio by 4: \(\overline{BC}\) = 3(4) = 12 units, \(\overline{AB}\) = 4(4) = 16 units, and \(\overline{AC}\)= 5(4) = 20 units. If the length of \(\overline{AB}\) is 16 units and the length of \(\overline{AC}\) is 20 units, AB is 4 less than \(\overline{AC}\), and the tangent of angle A is still 0.75, since \(\overline{BC}\) = 0.75. The length of \(\overline{BC}\) is 12 units.
If the sine of angle A is \(\frac{15}{17}\), what is the cosine of angle A?

The diagram is not to scale.
-
Solution
If the sine of angle A is \(\frac{15}{17}\), then the length of side BC is 15 and the length of side AC is 17, since the sine of an angle is equal to the side opposite the angle divided by the hypotenuse. Use the Pythagorean theorem to find the length of \(\overline{AB}\): (\(\overline{AB}\))2 + 152 = 172, (\(\overline{AB}\))2 + 225 = 289, (\(\overline{AB}\))2 = 64, \(\overline{AB}\) = 8. Since the cosine of an angle is equal to the side adjacent to the angle divided by the hypotenuse, the cosine of angle A is equal to = \(\frac{\overline{AB}}{\overline{AC}}=\frac{8}{17}\).
If the cosine of angle C is x⁄y, triangle ABC is not isosceles, and x does not equal y, which of the following is also equal to x⁄y?

The diagram is not to scale.
-
Solution
The sine of one base angle of a right triangle is equal to the cosine of the other base angle. Therefore, the sine of angle C is equal to the cosine of angle A, and the cosine of angle C is equal to the sine of angle A.Why? If the cosine of angle C is x⁄y,then the length of side BC is x and the length of side AC is y. Since the sine of angle A is equal to the side opposite angle A, side BC, divided by the hypotenuse, side AC, the sine of angle A is also x⁄y.
If line AB measures 3x – 6, line BC measures x2 – 2x, and line AC measures 2x + 2, what is the tangent of angle A?

The diagram is not to scale.
-
Solution
The tangent of an angle is equal to the side opposite the angle divided by the side adjacent to the angle;\(\frac{\overline{BC}}{\overline{AB}}=\frac{(x^{2}-2x)}{(3x+6)}=\frac{x(x-2)}{3(x-2)}=\frac{x}{3}\)
If angle B of isosceles triangle ABC is a right angle, what is the tangent of angle A?v
-
Solution
Since triangle ABC is an isosceles right triangle, the measures of both bases are equal. Therefore, the tangent of either angle A or angle C is the tangent of 45°, which is 1, since any number divided by itself is 1.
Triangle ABC is an equilateral triangle and triangle CDE is a right triangle. If the length of side AE is 20 units, what is the length of side BD?
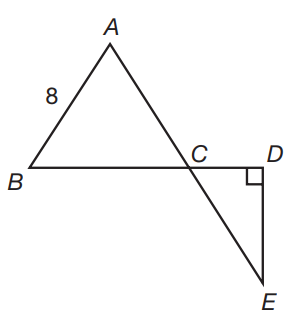
-
Solution
Side AB of equilateral triangle ABC is 8 units; therefore, side AC is also 8 units. Since side AE is 20 units, side CE must be 20 – 8 = 12 units. Angle ACB is 60°, since every angle of an equilateral triangle is 60°. Angles ACB and ECD are vertical angles, so angle ECD also measures 60°. Since angle ECD is 60°, angle CED is 30°, and triangle CDE is a 30-60-90 right triangle. Side CD is half the length of side CE, since it is the shorter base of the 30-60-90 right triangle. Therefore, side CD is equal to \(\frac{12}{2}\) = 6. Line segment BC is 8 units, since it is a side of equilateral triangle ABC, of which every side measures 8 units. The length of side BD is equal to the sum of side BC and side CD: 8 + 6 = 14 units.
If the sum of sides BC and AC is 12 units, what is the length of side AB?
Angle C measures 60°. The diagram is not to scale.
-
Solution
Since angle B of triangle ABC is a right angle and angle C is 60°, angle A must be 30° (180 – (90 + 60) = 30). Therefore, this is a 30-60-90 right triangle. Side AB is the longer base, since it is the side opposite the larger base angle. The hypotenuse of a 30-60-90 right triangle is twice the length of the shorter base. Therefore, if the length of side BC is x, then the length of side AC is 2x, and their sum is equal to 3x; 3x = 12, x = 4. The length of side BC is 4 units, and the length of side AB is 4√3 units, since the longer base of a 30-60-90 right triangle is √3 times the length of the shorter base.
If the hypotenuse of triangle ABC is 6x + 2 units long, what is the length of side AB?

Angle C measures 60°. The diagram is not to scale.
-
Solution
Since angle B of triangle ABC is a right angle and angle C is 60°, angle A must be 30° (180 – (90 + 60) = 30). Therefore, this is a 30-60-90 right triangle.Side AB is the longer base,since it is the side opposite the larger base angle. The hypotenuse of a 30-60-90 right triangle is twice the length of the shorter base. Therefore, the measure of side BC is \(\frac{(6x+2)}{2}\) = 3x + 1 units. The measure of the larger base of a 30-60-90 right triangle is √3 times the length of the shorter base. Therefore, the length of side AB is (3x + 1)√3 units.
If the length of side AB is 9 cm, what is the length of side BC?

Angle C measures 60°. The diagram is not to scale.
-
Solution
Since angle B of triangle ABC is a right angle and angle C is 60°, angle A must be 30° (180 – (90 + 60) = 30). Therefore, this is a 30-60-90 right triangle. Side AB is the longer base, since it is the side opposite the larger base angle. The measure of the larger base of a 30-60-90 right triangle is √3 times the length of the shorter base. Therefore, the length of side BC is equal to the length of side AB divided by √3:\(\frac{9}{\sqrt{3}}=\frac{9\sqrt{3}}{3}=3\sqrt{3}\) units.
Given right triangle ABC with right angle B, angle A is twice the size of angle C. If the measure of side AB is 7 units, what is the measure of side AC?
-
Solution
If angle A is twice the measure of angle C, then let angle C= x and let angle A= 2x; x+ 2x+ 90 = 180, 3x= 90, x= 30. The measure of angle C is 30° and the measure of angle A is 2(30) = 60°. Therefore, this is a 30-60-90 right triangle. Side AB is the shorter base, since it is the side opposite the smallest angle. The hypotenuse of a 30-60-90 right triangle is twice the length of the shorter base. Therefore, the measure of AC is 2(7) = 14 units.