-
Solution
Angle ACD is the 30° angle of 30-60-90 right triangle ACD. The sine of 30° is 1⁄2. Since the sine of an angle is equal to the side opposite the angle divided by the hypotenuse,1⁄2 = \frac{\overline{AD}}{20}, 2(\overline{AD}) = 20,\overline{AD} = 10 units. \overline{AD} is the side of the right triangle opposite the 30° angle; therefore, it is the shorter side of the right triangle. \overline{DC}, the longer side of the triangle, is 3 times the length of \overline{AC}: 10√3. Since the area of a rectangle is equal to its length times its width, the area of ABCD = (10)(10√3) = 100√3 square units.
The length of a rectangle is two less than three times its width. If the area of the rectangle is 96 cm2, what is the length of the rectangle?
-
Solution
If the width of the rectangle is x, then the length of the rectangle is 3x – 2. Since the area of a rectangle is equal to its length times its width, (x)(3x – 2) = 96, 3x2 – 2x = 96, 3x2 – 2x – 96 = 0, (3x + 16)(x – 6) = 0, and x = 6 (disregard the negative value of x since the width of rectangle cannot be negative. Since x = 6, the length of the rectangle is equal to 3(6) – 2 = 18 – 2 = 16 cm.
The perimeter of a square is 3x – 4 units. If the area of the square is 25 square units, what is the value of x?
-
Solution
The area of a square is equal to the length of one side of the square multiplied by itself. Therefore, the length of one side of this square is equal to the square root of the area: \sqrt{25} = 5 units. Since the length of every side of a square is the same, the perimeter of this square is (4)(5) = 20 units. Set 3x – 4 equal to 20 and solve for x: 3x – 4 = 20, 3x = 24, x = 8.
If the lengths of the sides of a square are halved, the area of the new square is
-
Solution
The area of a square is equal to the length of one side of the square multiplied by itself. Therefore, if the length of a side of a square is x, the area of the square is x2. If the sides of the square are halved, then the area of the square becomes (1⁄2x)(1⁄2x) = 1⁄4 x2. The area of the new square,1⁄4x2,
The area of a rectangle is x2 + 7x + 10 square units. If the length of the rectangle is x + 2 units,what is the width of the rectangle?
-
Solution
The area of a rectangle is equal to its length times its width. Therefore, the width of the rectangle is equal to its area divided by its length:\frac{(x^{2}+7x10)}{(x+2)}; x2 + 7x + 10 can be factored into (x + 2)(x + 5). Cancel the (x + 2) terms from the numerator and denominator of the fraction. The width of the rectangle is x + 5 units.
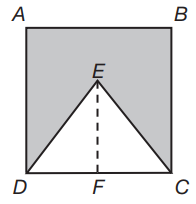
If the length of \overline{AB} of square ABCD is x units, and the length of \overline{EF} is 2⁄3 of \overline{AD}, what is the size of the shaded area?
-
Solution
The area of the square is x2 square units, since each side of the square has a length of x units. Since the height of the triangle is 2⁄3(x) and the base of the triangle is x, the area of the triangle is equal to:1⁄2(x)(2⁄3)x = 1⁄3x2 square units. Therefore, the size of the shaded area is equal to x2 – 1⁄3 (x)2 = 2⁄3(x)2 square units.
What is the area of an equilateral triangle that has a perimeter of 36 units?
-
Solution
Every side of an equilateral triangle is equal in length, so the length of one side of this triangle is \frac{36}{3} = 12 units. If a line is drawn from the vertex of an angle of the triangle to its opposite base, this line represents the height of the triangle. This line cuts the triangle into two identical 30-60-90 right triangles, since this line is perpendicular to the base, and every angle of an equilateral triangle is 60°. The length of this line is equal to the length of the longer base of a 30-60-90 right triangle, which is √3 times the length of the shorter base. The shorter base is equal to half the length of the hypotenuse. Since the hypotenuse is 12 units, the length of the shorter base is 6 units and the height is 63 units. Therefore, the area of the equilateral triangle is 1⁄2(12)(6√3) = (6)(6√3) = 36√3 square units.
Triangle DEC is inscribed in rectangle ABCD. If side AB = 30 units, side EC = 17 units, and side AE = side EB, what is the area of triangle DEC?

-
Solution
ABCD is a rectangle, which means that angle B is a right angle, and triangle EBC is a right triangle. Since \overline{AB}= 30 and \overline{AB} = \overline{AB}, then \overline{EB} = \frac{30}{2} = 15 units. The length of \frac{30}{2} can be found using the Pythagorean theorem: 152 + (\frac{30}{2})2 = 172, 225 + (\frac{30}{2})2 = 289, (\frac{30}{2})2 = 64, \frac{30}{2}= 8 units. Since AB = 30 units, \overline{DC} also equals 30 units, since alternate sides of rectangles are congruent.The base of triangle DEC is 30 units and the height of triangle DEC is 8 units. Therefore, the area of triangle DEC = 1⁄2(30)(8) = 1⁄2(240) = 120 square units.
An isosceles right triangle has a hypotenuse of x√6 units. What is the area of the triangle?
-
Solution
The hypotenuse of an isosceles right triangle is √2 times the length of a base of the triangle. Therefore, a base of this triangle measures \frac{x\sqrt{6}}{\sqrt{2}}= x√3 units. The length of one base of the isosceles right triangle is its height, so the area of the triangle is 1⁄2(x√3)(x√3) = 3⁄2(x)2 square units.
If the height of a triangle is half its base, b, what is the area of the triangle?
-
Solution
If the base the triangle is b, then the height of the triangle is 1⁄2b. The area of a triangle is equal to 1⁄2bh. Therefore, the area of this triangle is equal to 1⁄2(b(1⁄2b)) = 1⁄4b2.