Which of the following lines is perpendicular to the line given by the equation –2y = –8x + 10?
-
Solution
Divide both sides of the given equation by –2 to put the equation in slope-intercept form (y= mx + b); –2y = –8x + 10 is equivalent to y = 4x – 5. The slope of this line is the coefficient of x, 4. The slopes of perpendicular lines are negative reciprocals of each other. The negative reciprocal of 4 is –1⁄4. Only choice b is a line with a slope of –1⁄4.
Which of the following lines is parallel to the line given by the equation 4y = 6x – 6?
-
Solution
Divide both sides of the equation by 4 to put the given equation in slope-intercept form (y = mx + b); 4y = 6x – 6 is equivalent to y = 3⁄2 (x) – 3⁄2. The slope of this line is the coefficient of x, 3⁄2. Parallel lines have identical slopes. Only choice d is a line with a slope of 3⁄2.
Which of the following lines is perpendicular to the line given by the equation y = –1⁄6(x) + 8?
-
Solution
The slopes of perpendicular lines are negative reciprocals of each other. When an equation is written in slope-intercept form (y = mx + b), the slope of the line is m. The slope of the line y = –1⁄6(x) + 8 is –1⁄6. The negative reciprocal of –1⁄6 is 6. Only choice e is a line with a slope of 6.
Which of the following lines is parallel to the line given by the equation y = –2x + 4?
-
Solution
Parallel lines have identical slopes. When an equation is written in slope-intercept form (y = mx + b), the slope of the line is m. The slope of the line y = –2x + 4 is –2. Only choice a is a line with a slope of –2.
What is the slope of the line given by the equation 5y = –3x + 6?
-
Solution
Divide both sides of the equation by 5 to put the equation in slope-intercept form (y = mx + b); 5y = –3x + 6 is equivalent to y = –3⁄5 x + 6⁄5. The slope of this line is the coefficient of x, –3⁄5.
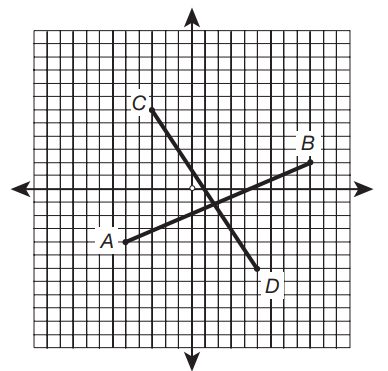
What is the distance from the point C to point D?
-
Solution
The coordinates of point C are (–3,6) and the coordinates of point D are (5,–6). To find the distance between two points, use the distance formula:
D = \(\sqrt{((x_{2}-x_{1})^{2}+(y_{2}+y_{1})^{2})}\)
D = \(\sqrt{((5-(-3))^{2}+((-6)-6)^{2})}\)
D = \(\sqrt{((5-(-3))^{2}+((-6)-6)^{2})}\)
D = \(\sqrt{((5-(-3))^{2}+((-6)-6)^{2})}\)
D = \(\sqrt{208}=\sqrt{16}\sqrt{13}=4\sqrt{13}\)units

What is the distance from the point A to point B?
-
Solution
The coordinates of point A are (–5,–4) and the coordinates of point B are (9,2). To find the distance between two points, use the distance formula:
D = \(\sqrt{((x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})}\)
D = \(\sqrt{((7-3)^{2}+((-6)-8)^{2})}\)
D = \(\sqrt{((7-3)^{2}+((-6)-8)^{2})}\)
D = \(\sqrt{16+196}\)
D = \(\sqrt{16+196}\) = √4\(\sqrt{58}\) = 2\(\sqrt{58}\)units
What is the distance from the point (3,8) to the point (7,–6)?
-
Solution
To find the distance between two points, use the distance formula:
D = \(\sqrt{((x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})}\)
D = \(\sqrt{((7-3)^{2})+((-6)-8)^{2}}\)
D = \(\sqrt{(4^{2}+(-14)^{2})}\)
D = \(\sqrt{(16+196)}\)
D = \(\sqrt{232}\) = √4\(\sqrt{53}\) = 2\(\sqrt{53}\) units
What is the distance from the point (0,–4) to the point (4,4)?
-
Solution
To find the distance between two points, use the distance formula:
D = \(\sqrt{((x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})}\)
D = \(\sqrt{((x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})}\)
D = \(\sqrt{((x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})}\)
D = \(\sqrt{(16+64)}\)
D = \(\sqrt{(16+64)}\) = \(\sqrt{16}\)√5=4√5 units
What is the distance from the point (–6,2) to the point (2,17)?
-
Solution
To find the distance between two points, use the distance formula:
\(D=\sqrt{((x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})}\)
\(D=\sqrt{((2-(-6))^{2}+(17-2)^{2})}\)
\(D=\sqrt{(8^{2}+(15)^{2})}\)
\(D=\sqrt{(8^{2}+(15)^{2})}\)
D=\(\sqrt{289}\)= 17 units