If the measure of angle 3 is 5x + 3 and the measure of angle 4 is 15x + 7, what is the sum of angles 5 and 6?
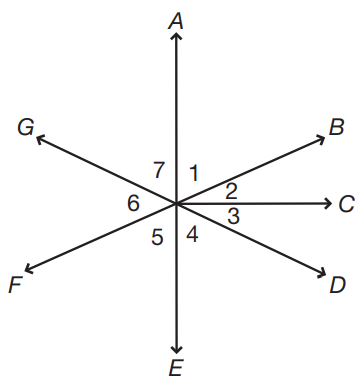
Lines AE, BF, GD, and ray OC all intersect at point O (not labeled), and line AE is perpendicular to ray OC.
-
Solution
Since line AE is perpendicular to ray OC, angle EOC is a right angle (measuring 90°). Angles 3 and 4 combine to form angle EOC; therefore, their sum is equal to 90°: 5x + 3 + 15x + 7 = 90, 20x + 10 = 90, 20x = 80, x = 4. Therefore, the measure of angle 4 is equal to: 15(4) + 7 = 67°. Angles 4, 5, and 6 form a line; therefore, the sum of their measures is 180°. If x is the sum of angles 5 and 6, then 67 + x = 180, and x = 113°.
If angle 1 measures 62° and angle 4 measures 57°, what is the measure of angle 6?

Lines AE, BF, GD, and ray OC all intersect at point O (not labeled), and line AE is perpendicular to ray OC.
-
Solution
Since line AE is perpendicular to ray OC, angle EOC is a right angle (measuring 90°). Angles 3 and 4 combine to form angle EOC; therefore, their sum is equal to 90°: 90 – 57 = 33. Angle 3 measures 33°. Angle AOC is also a right angle, with angles 1 and 2 combining to form that angle. Therefore, the measure of angle 2 is equal to: 90 – 62 = 28°. Angle 6 and angle BOD are vertical angles; their measures are equal. Since angles 2 and 3 combine to form angle BOD, the measure of BOD, and angle 6, is equal to: 33 + 28 = 61°
If the measure of angle 3 is 2x + 2 and the measure of angle 4 is 5x – 10, what is the measure of angle 7?

Lines AE, BF, GD, and ray OC all intersect at point O (not labeled), and line AE is perpendicular to ray OC.
-
Solution
Since line AE is perpendicular to ray OC, angle EOC is a right angle (measuring 90°). Angles 3 and 4 combine to form angle EOC; therefore, their sum is equal to 90°: 2x + 2 + 5x – 10 = 90, 7x – 8 = 90, 7x = 98, x = 14. Angle 4 is equal to 5(14) – 10 = 70 – 10 = 60°. Since angles 4 and 7 are vertical angles, their measures are equal, and angle 7, too, measures 60°.
Which of the following number sentences is NOT true?

Lines AE, BF, GD, and ray OC all intersect at point O (not labeled), and line AE is perpendicular to ray OC.
-
Solution
Since line AE is perpendicular to ray OC, angles AOC and EOC are both 90°. Since angles 1 and 2 combine to form angle AOC and angles 3 and 4 combine to form angle EOC, these sums must both equal 90°. Therefore, angle 1 + angle 2 = angle 3 + angle 4. Angles 1, 2, 3, and 7 form a line, as to angles 4, 5, and 6. Therefore, the measures of angles 1, 2, 3, and 7 add to 180°, as do the sum of the measures of angles 4, 5, and 6. In the same way, angles 2, 3, 4, and 5 form a line, so the sum of the measures of those angles is also 180°. Angles GOF and BOD are vertical angles. Therefore, their measures are equal. Since angle 6 is angle GOF and angles 2 and 3 combine to form angle BOD, the measure of angle 6 is equal to the sum of the measures of angles 2 and 3. However, the sum of angle 1 and angle 7 is not equal to the sum of angle 2 and angle 3. In fact, the sum of angles 2 and 3 is supplementary to the sum of angles 7 and 1, since angle 6 is supplementary to the sum of angles 7 and 1, and the sum of angles 2 and 3 is equal to the measure of angle 6.
Which of the following pairs of angles are complementary?

Lines AE, BF, GD, and ray OC all intersect at point O (not labeled), and line AE is perpendicular to ray OC.
-
Solution
Perpendicular lines cross at right angles. Therefore, angle AOC is 90°. Since angles 1 and 2 combine to form angle AOC, the sum of the measures of angles 1 and 2 must be 90°. Therefore, they are complementary angles.
If the measure of angle 2 is 8x + 10 and the measure of angle 6 is x2 – 38, what is the measure of angle 8?
-
Solution
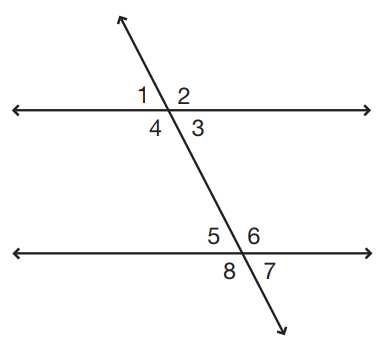
Angles 2 and 6 are alternating angles. Therefore, their measures are equal; 8x + 10 = x2 – 38, x2 – 8x – 48 = 0. Factor x2 – 8x – 48 and set each factor equal to 0; x2 – 8x – 48 = (x + 4)(x – 12), x + 4 = 0, x = –4; x – 12 = 0, x = 12. An angle cannot have a negative measure, so the –4 value of x must be discarded. If x = 12, then the measure of angle 2 is 8(12) + 10 = 106°. Notice that replacing x with 12 in the measure of angle 6 also yields 106: (12)2 – 38 = 144 – 38 = 106°. Since angles 6 and 8 are supplementary, the measure of angle 8 is equal to 180 – 106 = 74°.
Which of the following is NOT true if the measure of angle 3 is 90°?

-
Solution
If angle 3 measures 90°, then angles 1, 6, and 7 must also measure 90°, since they are alternating angles. Angles 3 and 4 are supplementary, since these angles form a line. Therefore, the measure of angle 4 is equal to 180 – 90 = 90°. Angles 3 and 4 are congruent and supplementary. Since angles 2, 4, 5, and 8 are alternating angles, they are all congruent to each other. Every numbered angle measures 90°. Therefore, every numbered angle is congruent and supplementary to every other numbered angle.Angles 5 and 7 are in fact adjacent, since they share a common vertex and a common ray. However, angles 1 and 2 are not complementary—their measures add to 180°, not 90°.
If the measure of angle 4 is 6x + 20 and the measure of angle 7 is 10x – 40, what is the measure of angle 6?

-
Solution
Angles 4 and 7 are alternating angles. Therefore, their measures are equal; 6x + 20 = 10x – 40, 4x = 60, x = 15. Since x = 15, the measure of angles 4 and 7 is 6(15) + 20 = 90 + 20 = 110. Notice that replacing x with 15 in the measure of angle 7 also yields 110: 10(15) – 40 = 150 – 40 = 110. Since angles 6 and 7 are vertical angles, the measure of angle 6 is also 110°.
If the measure of angle 5 is five times the measure of angle 6, what is the measure of angle 5?

-
Solution
Angles 5 and 6 are supplementary. Therefore, the sum of their measures is 180°. If the measure of angle 6 is x, then the measure of angle 5 is 5x; 5x + x = 180, 6x = 180, x = 30. The measure of angle 6 is 30°, and the measure of angle 5 is 5(30) = 150°.
If the measure of angle 2 is equal to 12x + 10 and the measure of angle 8 is equal to 7x – 1,what is the measure of angle 2?

-
Solution
Angles 2,4,6,and 7 are alternating (vertical) angles. Therefore, their measures are equal. Angles 7 and 8 are supplementary. Therefore, angles 2 and 8 are also supplementary; 12x + 10 + 7x – 1 = 180, 19x + 9 = 180, 19x = 171, x = 9. Since x = 9, the measure of angle 2 is 12(9) + 10 = 108 + 10 = 118°.