If the sum of the measures of angles 20 and 14 is 15x + 6, and the sum of the measures of angles 20 and 15 is 18x, what is the measure of angle 19?
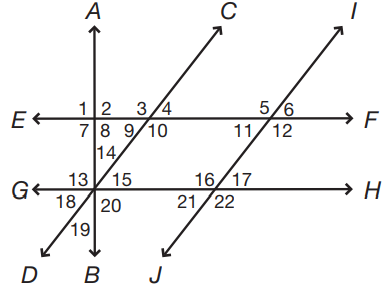
Lines EF and GH are parallel to each other, lines CD and IJ are parallel to each other, and line AB is perpendicular to lines EF and GH. Every numbered angle is greater than 0°.
-
Solution
Since lines AB and GH are perpendicular, angle 20 measures 90° and the sum of the measures of angles 14 and 15 is 90°. Therefore, angle 14 = 15x + 6 – 90 and angle 15 = 18x – 90. Since the sum of angles 14 and 15 is 90°, (15x + 6 – 90) + (18x – 90) = 90, 33x – 174 = 90, 33x = 264, x = 8. Therefore, the sum of angles 20 and 14 is 15(8) + 6 = 126, and the measure of angle 14 is equal to: 126 – 90 = 36. Since angles 14 and 19 are vertical angles, angle 19 also measures 36°.
If angle 5 = 8x – 4 and angle 22 = 7x + 11, what is the measure of angle 16?

Lines EF and GH are parallel to each other, lines CD and IJ are parallel to each other, and line AB is perpendicular to lines EF and GH. Every numbered angle is greater than 0°.
-
Solution
Angles 5, 12, 16, and 22 are alternating (vertical) angles; their measures are equal; 8x – 4 = 7x + 11, x – 4 = 11, x = 15; 8(15) – 4 = 120 – 4 = 116°. Notice that you could also substitute 15 into the measure of angle 22: 7(15) + 11 = 105 + 11 = 116°. The measure of angles 5, 12, 16, and 22 is 116°.
Which of the following must be true?

Lines EF and GH are parallel to each other, lines CD and IJ are parallel to each other, and line AB is perpendicular to lines EF and GH. Every numbered angle is greater than 0°.
-
Solution
Angles 1 and 8 are both right angles. In addition to be equal, they are also supplementary, since 90 + 90 = 180°. Angles 19, 15, and 20 also add to 180°, since these angles form a line. Angle 1 + angle 8 = angle 19 + angle 15 + angle 20 = 180°
If the sum of the measures of angles 21 and 5 is x2 + 11 and the measure of angle 3 is 9x + 1, what is the measure of angle 10?

Lines EF and GH are parallel to each other, lines CD and IJ are parallel to each other, and line AB is perpendicular to lines EF and GH. Every numbered angle is greater than 0°.
-
Solution
Angles 21, 17, and 11 are alternating angles; their measure are equal. Since angle 11 and angle 5 are supplementary (they combine to form a line), angles 21 and 5 must be supplementary. Therefore, x2 + 11 = 180, x2 = 169,(x + 13)(x – 13) = 0, and x = 13 (disregard the negative value of x, since every numbered angle is greater than 0). If x = 13, then the measure of angle 3 is 9(13) + 1 = 117 + 1 = 118°. Since angle 3 and angle 10 are vertical angles, angle 10 is also 118°.
If the sum of the measures of angles 8 and 9 is 133°, what is the measure of angle 3?

Lines EF and GH are parallel to each other, lines CD and IJ are parallel to each other, and line AB is perpendicular to lines EF and GH. Every numbered angle is greater than 0°.
-
Solution
Since lines EF and AB are perpendicular, angle 8 measures 90°. Therefore, 90 + angle 9 = 133°,133 – 90 = 43, so angle 9 measures 43°. Angles 3 and 9 form a line; the sum of their measures is 180°. The measure of angle 3 is equal to: 180 – 43 = 137°.